Giải và biện luận phương trình bậc 2 theo tham số m. Phương trình bậc 2 một ẩn là một trong những dạng toán hay gặp trong các đề thi vào lớp 10, đặc biệt là dạng toán giải và biện luận phương trình bậc 2 theo tham số m làm nhiều em gặp khó khăn vì không nắm vững được cách giải.
Bài viết dưới đây sẽ trình bày chi tiết cách giải và biện luận phương trình bậc 2 theo tham số m ở chương trình toán lớp 9 để các em cảm thấy việc giải dạng toán này cũng không hề khó nhằn như nhiều em vẫn nghĩ.
A. Cách giải và biện luận phương trình bậc 2 theo tham số m
• Giải phương trình bậc 2 dạng: ax2 + bx + c = 0 (a ≠ 0)
Để giải phương trình bậc 2, điều đầu tiên các em cần nhớ là công thức tính biệt thức delta: Δ = b2 – 4ac
– Nếu Δ > 0 thì phương trình có hai nghiệm phân biệt:
![]()
![]()
– Nếu Δ = 0 thì phương trình có nghiệm kép:
![]()
– Nếu Δ < 0 thì phương trình vô nghiệm.
> Lưu ý: Nếu hệ số b của phương trình bậc 2 là số chẵn (tức b = 2b’) ta có thể tính biệt thức Δ’ để giải biện luận phương trình.
Δ’ = b’2 – ac
Nếu Δ’ > 0 thì phương trình có hai nghiệm phân biệt:
![]()
Nếu Δ’ = 0 thì phương trình có nghiệm kép:
![]()
Nếu Δ’ < 0 thì phương trình vô nghiệm.
• Cách giải và biện luận phương trình bậc 2 có chứa tham số m
Xét các trường hợp của hệ số a:
+ Nếu a = 0 thì tìm nghiệm của phương trình bậc nhất.
+ Nếu a ≠ 0 thì thực hiện các bước sau:
– Bước 1: Tính biệt thức delta (hoặc Δ’)
– Bước 2: Xét các trường hợp của delta chứa tham số
– Bước 3: Tìm nghiệm của phương trình theo tham số
B. Bài tập minh họa Giải và biện luận phương trình bậc 2 theo tham số m
* Bài tập 1: Giải và biện luận phương trình bậc 2 theo tham số m sau:
x2 – 2(3m – 1)x + 9m2 – 6m – 8 = 0 (*)
* Lời giải:
Để ý phương trình (*) có các hệ số: a = 1; b = 2(3m – 1) và c = 9m2 – 6m – 8
Vì vậy ta tính biệt số Δ’, ta có:
Δ’ = b’2 – ac = (3m – 1)2 – 1.(9m2 – 6m – 8)
= 9m2 – 6m + 1 – 9m2 + 6m + 8
= 9 > 0
Suy ra: 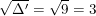
Nên sao có 2 nghiệm phân biệt:
![]()
![]()
→ Kết luận: Với mọi tham số m thì pt (*) luông có 2 nghiệm phân biệt.
* Bài tập 2: Giải và biện luận phương trình bậc 2 sau theo tham số m:
3x2 – mx + m2 = 0
* Lời giải:
Các hệ số của phương trình bậc 2 trên: a = 3; b = -m; c = m2
Tính biệt thức delta:
Δ = b2 – 4ac = (-m)2 – 4.3.m2 = m2 – 12m2 = -11m2 ≤ 0 (với mọi m)
+ Trường hợp: Δ = 0 ⇔ -11m2 = 0 ⇔ m = 0
Phương trình (*) có nghiệm kép: x1 = x2 = 0
+ Trường hợp: Δ < 0 ⇔ -11m2 < 0 ⇔ m ≠ 0
Phươn trình (*) vô nghiệm.
→ Kết luận: Với m = 0 pt (*) có nghiệm kép x = 0
Với m ≠ 0 pt (*) vô nghiệm
* Bài tập 3: Cho phương trình mx2 – 2(m – 1)x + (m + 1) = 0 (*) với m là tham số.
a) Giải phương trình với m = -2.
b) Tìm m để phương trình (*) có 2 nghiệm phân biệt.
c) Tìm m để phương trình (*) có 1 nghiệm.
* Lời giải:
a) Với m = -2, pt (*) trở thành: -2x2 – 2(-2 – 1)x + (-2 + 1) = 0
⇔ -2x2 + 6x – 1 = 0
⇔ 2x2 – 6x + 1 = 0
Tính biệt số delta (các em có thể tính delta phẩy sẽ gọn hơn nhé):
Δ = b2 – 4ac = (-6)2 – 4(2.1) = 36 – 8 = 28 > 0
Suy ra 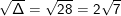
Phương trình có 2 nghiệm phân biệt:
![]()
![]()
b) Phương trình (*) có 2 nghiệm phân biệt khi: ![]()
Δ’ = b’2 – ac = (m – 1)2 – m(m + 1)
= m2 – 2m + 1 – m2 – m
= -3m + 1
Δ’ > 0 ⇔ -3m + 1 > 0 ⇔ m <1/3
Vậy phương trình (*) có 2 nghiệm khi chỉ khi: 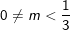
c) Với m = 0: Pt(*) có dạng pt bậc nhất một ẩn: 2x + 1 = 0.
Khi đó pt có nghiệm duy nhất x = -1/2
Với m ≠ 0: pt(*) là pt bậc 2 một ẩn, có 1 nghiệm khi Δ’ = 0
⇔ -3m + 1 = 0 ⇔ m = 1/3
Kết luận: Phương trình (*) có nghiệm duy nhất khi m = 0 hoặc m = 1/3.
* Bài tập 4: Giải và biện luận phương trình bậc 2 chứa tham số m sau:
(m – 1)x2 – 2mx + m + 2 = 0 (*)
* Lời giải:
Để ý pt(*) có các hệ số: a = (m – 1); b = (-2m); c = (m + 2)
+ Xét trường hợp a = 0, nghĩa là (m – 1) = 0 tức m = 1, ta có:
pt(*) trở thành: -2x + 3 = 0 ⇒ x = 3/2.
+ Xét trường hợp a ≠ 0 (m – 1 ≠ 0) tức m ≠ 1, ta có:
Δ’ = m2 – (m – 1).(m + 2)
= m2 – (m2 + 2m – m – 2)
= m2 – m2 – m + 2
= -m + 2
– Nếu Δ’ > 0 ⇔ -m + 2 > 0 ⇔ m < 2 thì pt có 2 nghiệm phân biệt:
![]()
– Nếu Δ’ = 0 ⇔ -m + 2 = 0 ⇔ m = 2 thì pt có nghiệp kép:
– Nếu Δ’ < 0 ⇔ -m + 2 < 0 ⇔ m > 2 thì pt vô nghiệm
→ Kết luận:
Với m = 1 hoặc m = 2 phương trình (*) có nghiệm duy nhất.
Với m < 2 phương trình (*) có 2 nghiệm phân biệt
Với m > 2 phương trình (*) vô nghiệm
* Bài tập 5: Giải và biện luận các phương trình sau theo tham số k:
a) (k – 1)x2 + 3kx + 2k + 1 = 0
b) kx2 + 2k2x + 1 = 0
* Bài tập 6: Giải và biện luận các phương trình sau theo tham số m:
a) x2 – 2(m – 4)x + m2 = 0
b) (2m – 7)x2 + 2(2m + 5)x – 14m + 1 = 0
Hy vọng với bài viết Giải và biện luận phương trình bậc 2 theo tham số m ở trên giúp các em giải các bài tập dạng này một cách dễ dàng. Mọi góp ý và thắc mắc các em hãy để lại nhận xét dưới bài viết để ghi nhận và hỗ trợ, chúc các em học tốt.
Đăng bởi: Thcs-thptlongphu.edu.vn
Chuyên mục: Tổng hợp





