Phép đối xứng tâm là gì? Các dạng toán của phép đối xứng tâm

Phép đối xứng tâm là gì? Các dạng toán của phép đối xứng tâm

Phép đối xứng tâm là một trong những phần kiến thức Hình học quan trọng các bạn đã được tìm hiểu trong chương trình Hình học 11. Bài viết hôm nay, sẽ hệ thống lại tất cả các kiến thức cốt yếu và liên quan đến chuyên đề này cùng các dạng toán thường gặp của phép đối xứng tâm. Bạn dành thời gian chia sẻ nhé !

I. LÝ THUYẾT VỀ PHÉP ĐỐI XỨNG TÂM

1. Định nghĩa

Bạn đang xem: Phép đối xứng tâm là gì? Các dạng toán của phép đối xứng tâm

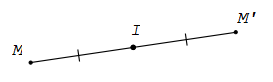
    Cho điểm I. Phép biến hình biến điểm I thành chính nó, biến mỗi điểm M khác I thành M’ sao cho I là trung điểm của MM’ được gọi là phép đối xứng tâm I.

    Điểm I được gọi là tâm đối xứng.

    Phép đối xứng tâm I thường được kí hiệu là Đ_I.

    Nếu hình H là ảnh của hình H qua Đ_I thì ta còn nói H đối xứng với H’ qua tâm I, hay H và H’ đối xứng với nhau qua I.

    Từ đinh nghĩa suy ra M = Đ_I(M) ⇔ IM’→ = – IM→

2. Biểu thức toạ độ

    Với O(0;0), ta có M(x’; y’) = Đ_O[M(x;y)] thì

        

    Với I(a; b), ta có M(x’; y’) = Đ_I(x’; y’) thì

        

3. Tính chất

Tính chất 1

    Nếu Đ_I(M) = M’ và Đ_I(N) = N thì M’N’→ = – MN→, từ đó suy ra M’N’ = MN.

Tính chất 2

    Phép đối xứng tâm biến đường thẳng thành đường thẳng song song hoặc trùng với nó, biến đoạn thẳng thành đoạn thẳng bằng nó, biến tam giác thành tam giác bằng nó, biến đường tròn thành đường tròn cùng bán kính.

4. Tâm đối xứng của một hình

Định nghĩa

    Điểm I được gọi là tâm đối xứng của hình H nếu phép đối xứng tâm I biến hình H thành chính nó.

    Khi đó ta nói H là hình có tâm đối xứng.

II. CÁC DẠNG TOÁN CỦA PHÉP ĐỐI XỨNG TÂM

Dạng 1: Xác định ảnh của một hình qua phép đối xứng tâm

Phương pháp giải: Sử dụng biểu thức tọa độ và các tính chất của phép đối xứng tâm

Ví dụ : Trong mặt phẳng Oxy cho điểm A (-1; 3) và đường thẳng d có phương trình: x – 2y + 3 = 0 . Tìm ảnh của A và d qua phép đối xứng tâm O ( với O là gốc tọa độ)

Lời giải

Gọi A’ (x’; y’) là ảnh của A qua phép đối xứng tâm O (0; 0). Theo công thức tọa độ của phép đối xứng ta có

x’=0-x Suy ra x=-x’

y’=0-x Suy ra y= -ý

x’=1, y’=3 Suy ra A'(1;-3)

Gọi M (x; y) là một điểm bất kỳ thuộc d và M’ (x’; y’) là một điểm bất kỳ thuộc d’ là ảnh của d qua phép đối xứng tâm O. Theo công thức tọa độ của phép đối xứng ta có:

x’=0-x Suy ra x=-x’

y’=0-x Suy ra y= -ý

Suy ra (-x’)-2(-y’)+3=0

Sy ra x’-2y’-3=0

Do đó d’ có phương trình x – 2y – 3 = 0

Dạng 2: Xác định tâm đối xứng khi biết ảnh và tạo ảnh

Ví dụ : Cho đường thẳng d: x – 2y + 2 = 0 và d’: x – 2y – 8 = 0. Tìm phép đối xứng tâm biến d thành d’ và biến trục Oy thành chính nó

Lời giải

Giao của hai đường thẳng d : x – 2y + 2 = 0 và d ‘: x – 2y – 8 = 0 với trục Oy là A (0; 1), A’ (0; – 4)

Theo giả thiết biến d thành d’ và biến trục Oy thành chính nó thì A biến thành A’ nên tâm đối xứng là I trung điểm của AA’ là I(0;-3/2) 

Dạng 3: Tìm tâm đối xứng của một hình

Phương pháp giải: Điểm I được gọi là tâm đối xứng của hình H nếu phép đối xứng tâm I biến hình H thành chính nó. Khi đó ta nói H là hình có tâm đối xứng.

Ví dụ : Tìm tâm đối xứng biến điểm A (4; 3) thành điểm A’ (6; 1).

Lời giải

I (a; b) là trung điểm của AA’ $\Rightarrow$a=4+6/2=5

b=3+1/2=2

Vậy tâm đối xứng cần tìm là I (5; 2)

Dạng 4: Sử dụng phép đối xứng tâm để giải các bài toán dựng hình

Phương pháp giải:  Xem điểm cần dựng là giao của một đường có sẵn và ảnh của một đường khác qua phép quay D1 nào đó

Ví dụ: Cho hai đường thẳng d, d’ và điểm I. Tìm điểm A trên d và điểm B trên d’ sao cho I là trung điểm của đoạn thẳng AB

Lời giải

-Dựng đường thẳng d1 là ảnh của d qua phép đối xứng tâm I

-Dựng giao điểm B của d’ và d1

-Dựng A là giao điểm của đường thẳng BI và đường thẳng d

Số nghiệm hình là số giao điểm của đường thẳng d1 và d’

– Nếu d’ và d1 song song thì bài toán vô nghiệm

-Nếu d’ và d1 cắt nhau thì bài toán có 1 nghiệm

-Nếu d’ và d1 trùng nhau thì bài toán có vô số nghiệm

Dạng 5: Sử dụng phép đối xứng tâm để giải bài toán tập hợp điểm

Phương pháp giải: Để tìm quỹ tích (tập hợp điểm), nếu có phép đối xứng tâm O biến điểm M thành M’ và (C) là tập hợp điểm của M thì ảnh (C’) qua tâm đối xứng tâm O là tập hợp của M’

Ví dụ : Cho trên đường tròn (O)  hai điểm cố định B, C và một điểm A thay đổi. Gọi H là trực tâm của tam giác ABC và H’ là điểm sao cho tứ giác BHCH’ là hình bình hành. Chứng minh rằng khi A thay đổi thì H’ luôn nằm trên đường tròn (O). Tìm tập hợp của H

Lời giải

Gọi A’ là điểm xuyên tâm đối của A trên (O). Ta có:

A’B $\perp$AB (ABA’ là tam giác có cạnh huyền là đường kính)

CH $\perp$AB (do CH là đường cao)

Nên AB // CH (1)

Tương tự ta chứng minh được A’C // BH (2)

(1) và (2)$\Rightarrow$ BHCA’ là hình bình hành

$\Rightarrow$Lấy H’ trung với A’. Vậy BHCH’ là hình bình hành và H’ luôn nằm trên đường tròn.

Trong hình bình hành BHCH’, có HH’ và BC là hai đường chéo nnen HH’ nhận trung điểm I của BC cố định làm trung điểm.

Do đó H là điểm đối xứng với H’ qua I.

Mà H’ $\in$(O) nên H$\in$ một đường tròn đối xứng với (O) qua I

Ví dụ: Một hình bình hành ABCD có hai đỉnh A, C cố định, còn đỉnh B thay đổi trên đường thẳng d. Tìm quỹ tích đỉnh D

Lời giải

Vì ABCD là hình bình hành có hai đỉnh A, C cố định nên tâm O là trung điểm của đường chéo AC

Suy ra: O cố định

Mà tâm O là trung điểm đường chéo BD. Do đó phép đối xứng tâm O biến B thành D

Mà B chạy trên đường thẳng d nên điểm D chạy trên đường thẳng d’ ảnh của d qua phép đối xứng tâm O

Ngược lại với mọi điểm D thuộc đường thẳng d’ ta luôn tìm được điểm B thuộc d sao cho O là trung điểm của BD

Vậy quỹ tích của các điểm D là đường thẳng d’ ảnh của d qua phép đối xứng tâm O

III. BÀI TẬP VẬN DỤNG

Bài 1: Cho hình bình hành MNPQ nội tiếp hình bình hành ABCD (4 đỉnh nằm trên bốn cạnh). Chứng minh hai hình bình hành có cùng tâm đối xứng

Bài 2: Xác định ảnh qua phép đối xứng tâm I (4; -7) của:

a. Điểm A (3; -2) của đường thẳng d: 3x – 6y + 1 = 0

Bài 3: Tìm ảnh qua phép đối xứng tâm I (-3; 5) của:

a. Điểm A (3; -4)

b. Đường thẳng d: 2x – y +1 = 0

Bài 4: Cho phép đối xứng tâm I (p; 3). Tìm ảnh của đồ thị hàm số (C): y = 2sin2x – 5

Bài 5: Giả sử phép đối xứng tâm D₀ biến đường thẳng d thành đường thẳng d’. Chứng minh nếu d không đi qua tâm đối xứng O thì d’ song song với d, O cách đều d và d’

Bài 6: Trong mặt phẳng hệ tọa độ Oxy, tìm tọa độ điểm M’ là ảnh của điểm M (2; 1) qua phép đối xứng tâm I (3; -2)

Bài 7: Một hình bình hành ABCD có hai đỉnh A, C cố định, còn đỉnh B thay đổi trên đường tròn (O; R) . Tìm quỹ tích của đỉnh D

Bài 8: Tìm tâm đối xứng của các hình sau đây: tam giác đều, hình bình hành, lục giác đều, đường tròn, hình gồm hai đường tròn bằng nhau

Bài 9: Cho đường tròn (O) và dây cung AB cố định, M là một điểm di động trên (O), M không trùng với A, B. Hai đường tròn (O1), (O2) cùng đi qua M và tiếp xúc với AB tại A và B. Gọi N là giao điểm thứ hai của (O1) và (O2). Tìm tập hợp điểm N khi M di động

Bài 10: Tìm tâm đối xứng biến điểm A (5; 0) thành điểm A’ (8; 8)

Vậy là các bạn vừa được chia sẻ chuyên đề về phép đối xứng tâm và các dạng toán thường gặp của phép đối xứng tâm. Hi vọng, đây sẽ nguồn tư liệu hữu ích giúp các bạn dạy và học tốt hơn. Xem thêm chuyên đề về phép tịnh tiến nữa bạn nhé !