Tích phân là gì? Các công thức tính tích phân đầy đủ & nhiều dạng bài tập

Tích phân là gì? Các công thức tính tích phân đầy đủ & nhiều dạng bài tập

Tích phân là gì? Các công thức tính tích phân đầy đủ & nhiều dạng bài tập thường gặp là những mảng kiến thức trọng tâm sẽ chia sẻ cùng quý bạn đọc qua bài viết sau đây. Bạn dành thời gian chia sẻ để nắm vẵng hơn mảng kiến thức Toán 12 vô cùng quan trọng này nhé !

I. TÍCH PHÂN LÀ GÌ ?

1. Khái niệm tích phân

Bạn đang xem: Tích phân là gì? Các công thức tính tích phân đầy đủ & nhiều dạng bài tập

* Định nghĩa:

Cho hàm số f liên tục trên K và a, b là hai số bất kì thuộc K. Nếu F là một nguyên hàm của f trên K thì hiệu số:

F(b) – F(a)

Được gọi là tích phân của f từ a đến b và kí hiệu:

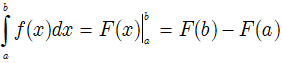
* Nhận xét: Tích phân của hàm số f từ a đến b có thể kí hiệu bởi 

Tích phân đó chỉ phụ thuộc vào f và các cận a; b mà không phụ thuộc vào cách ghi biến số.

* Định lí: Cho hàm số y = f(x) liên tục; không âm trên đoạn [a;b]. Khi đó, diện tích S của hình thang cong giới hạn bởi đồ thị hàm số y = f(x); trục hoành và hai đường thẳng x = a; x = b là:

2. Tính chất của tích phân

Giả sử cho hai hàm số f(x) và g(x) liên tục trên K và a, b, c là ba số bất kỳ thuộc K. Khi đó ta có :

 

II. CÁC CÔNG THỨC TÍNH TÍCH PHÂN ĐẦY ĐỦ NHẤT

Cho các hàm số là f(x), g(x) liên tục trên K. Trong đó a,b,c là những số thuộc K. Khi đó công thức của tích phân sẽ được biểu thị qua bảng sau:

III. CÁC PHƯƠNG PHÁP TÍNH TÍCH PHÂN

Hiện nay có rất nhiều phương pháp khác nhau để giải các bài toán tích phân dó đó bạn đọc có thể tham khảo và áp dụng. Cụ thể:

1. Phương pháp tích phân từng phần

a. Định lí

Nếu u(x) và v(x) là các hàm số có đạo hàm liên tục trên [a;b] thì:

b. Phương pháp chung

• Bước 1: Viết f(x)dx dưới dạng udv = u.v’dx bằng cách chọn một phần thích hợp của f(x) làm u(x) và phần còn lại dv = v'(x)dx

• Bước 2: Tính du = u’dx và v = ∫dv = ∫v'(x)dx

• Bước 3: Tính 

* Cách đặt u và dv trong phương pháp tích phân từng phần.

2. Phương pháp vi phân

3. Phương pháp đổi biến số

3.1. Phương pháp đổi biến số dạng 1

Định lí

Nếu:

1) Hàm x = u(t) có đạo hàm liên tục trên [α;β].

2) Hàm hợp f [u(t)] được xác định trên [α;β].

3) u(α) = a; u(β) = b.

Khi đó: 

 

Phương pháp chung

• Bước 1: Đặt x = u(t).

• Bước 2: Tính vi phân hai vế: x = u(t) ⇒ dx = u'(t)dt.

Đổi cận: 

• Bước 3: Chuyển tích phân đã cho sang tích phân theo biến t.

Vậy:

3.2. Phương pháp đổi biến dạng 2

Định lí

Nếu hàm số u = u(x) đơn điệu và có đạo hàm liên tục trên đoạn [a;b] sao cho f(x)dx = g(u(x))u'(x)dx = g(u)du thì:

Phương pháp chung

• Bước 1: Đặt u = u(x) ⇒ du = u’(x)dx

• Bước 2: Đổi cận: 

• Bước 3: Chuyển tích phân đã cho sang tích phân theo u.

Vậy:

IV. MỘT SỐ DẠNG TOÁN THƯỜNG GẶP

Bài 1. Cho tích phân . Tính tích phân 

A . I= 40    B. I= 10    C. I= 20    D. I= 5

Hướng dẫn:

Đáp án: B

Đặt 

Đổi cận: với x = 0 => t = 0

Với x = 6 => t = 3

Ta có:

Suy ra: 

Bài 2. Cho hàm số y= f(x) liên tục trên đoạn [0; 6] thỏa mãn  và  . Tính giá trị của biểu thức 

A. P= 4    B. P= 16    C. P= 8    D. P= 10

Hướng dẫn:

Đáp án: A

Ta có:

  

Bài 3. Tích phân  bằng

A.I=1    B.I= 2    C.I= 3    D. I= −1

Hướng dẫn:

Đáp án: A

Bai 4. Có bao nhiêu giá trị của m sao cho  :

A.1    B. 2    C. 3    D. 4

Hướng dẫn:

Đáp án: A

Ta có:

   

Vậy có 3 giá trị của m thỏa mãn.

Bài 5. Tích phân  bằng

 

Hướng dẫn:

Đáp án: D

Bài 6. Tích phân  bằng

 

Hướng dẫn:

Đáp án: B

Ta có:

Bài 7. Tính 

 

Hướng dẫn:

Đáp án: C

Bài 8. Tính 

 

Hướng dẫn:

Đáp án: B

Bài 9. Tích phân  có giá trị là

 

Hướng dẫn:

Đáp án: B

 

Bài 10. Tích phân  có giá trị là

 

Hướng dẫn:

Đáp án: A

Ta có

 

Bài viết trên đây, chúng tôi đã giới thiệu đến quý thầy cô và các bạn chuyên đề về tích phân, các công thức tính tích phân đầy đủ & nhiều dạng bài tập thường gặp. Hi vọng, đây là nguồn tư liệu hữu ích giúp các bạn dạy và học tốt hơn. Xem thêm định lí hàm Cos và nhiều kiến thức liên quan khác bạn nhé !