Tính chất của dãy tỉ số bằng nhau: Lý thyết và các dạng toán
Tính chất của dãy tỉ số bằng nhau là một trong những phần chương trình trọng tâm trong Toán 7, phân môn Đại số. Bài viết hôm nay, sẽ giúp bạn tổng hợp lại tất cả các kiến thức liên quan cần ghi nhớ. Cùng tìm hiểu ngay nhé !
I. LÝ THUYẾT VỀ TÍNH CHẤT CỦA DÃY TỈ SỐ BẰNG NHAU
1. Tính chất:
Bạn đang xem: Tính chất của dãy tỉ số bằng nhau: Lý thyết và các dạng toán
Tính chất của dãy tỉ số bằng nhau (với điều kiện các biểu thức có nghĩa)
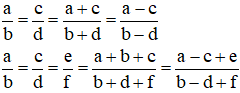
2. Phương pháp giải
Để tìm hai số x và y biết tổng x + y = s hoặc hiệu x – y = d và tỉ số ta làm như sau:

Áp dụng tính chất của dãy tỉ số bằng nhau:

3. Ví dụ:
Dùng dãy tỉ số bằng nhau để thể hiện câu nói sau: Số học sinh của ba lớp 7A, 7B, 7C tỉ lệ với các số 8; 9; 10
Lời giải
Ta có: Gọi số học sinh của ba lớp 7A, 7B, 7C lần lượt là x, y, z (học sinh)
Theo giả thiết có dãy tỉ số sau:


II. CÁC DẠNG TOÁN VỀ TÍNH CHẤT DÃY TỈ SỐ BẰNG NHAU
Dạng 1: Tìm một hoặc nhiều số hạng chưa biết trong dãy tỉ lệ thức
Phương pháp giải:
+ Nếu có 2 tỉ số bằng nhau thì dùng tính chất tỉ lệ thức
+ Nếu có 1 dãy tỉ số bằng nhau thì:
- Dùng trực tiếp tính chất dãy tỉ số bằng nhau
- Đặt tỉ số chung, biểu diễn các số hạng chưa biết qua tỉ số chung, thay vào giả thiết để tính
- Dùng tính chất dãy tỉ số nâng cao với các bài có bình phương hoặc lập phương
Ví dụ:
Tìm hai số x, y biết  và x + y = -32
và x + y = -32

Dạng 2: Tính giá trị biểu thức
Ví dụ. Cho a, b, c là các số hữu tỉ khác 0 sao cho:

Tìm giá trị bằng số của biểu thức:

Dạng 3: Chứng minh đẳng thức
Phương pháp giải:
- Phương pháp 1: Dùng tính chất tỉ lệ thức (nhân chéo, chứng minh tích bằng nhau)
- Phương pháp 2: Đặt k là giá trị chung, biểu diễn các đại lượng theo k, thay vào 1 hoặc 2 vế để biến đổi ra cùng kết quả.
- Phương pháp 3: Sử dụng tính chất dãy tỉ số bằng nhau
Chứng minh rằng nếu a + c = 2bd và 2bd = c(b+d)

Bài giải:
Ta có:
Từ và
(t/c phân phối).
(rút gọn cả 2 vế cho cd).
(t/c cơ bản của tỉ lệ thức).
Dạng 4: Áp dụng tính chất của dãy tỉ số bằng nhau để giải các bài toán
Ví dụ: Tìm diện tích của một hình chữ nhật có tỉ số giữa hai cạnh của nó bằng 2/3 và chu vi bằng 40m.Bài giải:
Bài giải:
Gọi x (m) là chiều rộng, y (m) là chiều dài ( x, y >0)
Tỉ số giữa hai cạnh là 2/3 nên suy ra x/y=2/
Theo tính chất của dãy tỉ số bằng nhau, ta có:
x/2=y/3=x+y/2+3=40/5=8
Do đó: x=16
y=24
Vậy diện tích hình chữ nhật là: S = 16.24 = 384 (m2)
III. BÀI TẬP TÍNH CHẤT DÃY TỈ SỐ BẰNG NHAU
Bài 1. Chia số 12 thành 4 phần tỉ lệ với các số 3, 5, 7, 9.
Bài 2: Các cạnh của một tam giác có số đo tỉ lệ với các số 3, 5, 7. Tính mỗi cạnh của tam giác đố, biết chu vi của nó là 40,5 cm.
Bài 3:

Bài 4: Tìm các số x, y, z, t, biết rằng:
x : y : z : t = 15 : 7 : 3 : 1 và x – y + z – t = 10.
Bài 5: Tìm các số x, y, z, t biết rằng:

Bài 6: Tìm các số a, b, c sao cho:
2a = 3b, 5b = 7c và 3a + 5c – 7b = 30.
Bài 7: Tìm x, y, z biết rằng:
x : y : z = 3 : 8 : 5 và 3x + y – 2z = 14.
Bài 8: Tìm một số có 3 chữ số, biết rằng số đó chia hết cho 18 và các chữ số của nó tỉ lệ với ba số 1; 2; 3.
Bài 9: Ba máy bơm cùng bơm nước vào một bể bơi có dung tích 235m³. Biết rằng thời gian để bơm được 1m³ nước của ba máy lần lượt là 3 phút, 4 phút, 5 phút. Hỏi mỗi máy bơm được bao nhiêu mét khối nước thì đầy bể?
Bài 10: Ba lớp 7 có tất cả 153 học sinh. Số học sinh lớp 7B bằng 8/9 số học sinh lớp 7A, số học sinh lớp 7C bằng 17/16 số học sinh lớp 7B. Tính số học sinhh của mỗi lớp.
Bài 11: Tỉ số của hai số bằng 4 : 5. Nếu thêm 1,2 vào số thứ nhất thì tỉ số của chúng sẽ bằng 11 : 15. Tìm hai số đó.
Bài 12:

Bài 13: Diện tích một tam giác bằng 27cm². Biết rằng tỉ số giữa một cạnh và đường cao tương ứng của tam giác bằng 1,5. Tính độ dài cạnh và đường cao nói trên.
Bài 14:

Vậy là các bạn vừa được tìm hiểu các tính chất của dãy tỉ số bằng nhau: Lý thyết và các dạng toán. Hi vọng, sau khi chia sẻ cùng bài viết bạn đã nắm vững hơn phần kiến thức Đại số 7 rất quan trọng này. Chuyên đề về tỉ lệ thức cũng đã được giới thiệu rất chi tiết. Bạn nhớ tham khảo thêm nhé !
Đăng bởi: Thcs-thptlongphu.edu.vn
Chuyên mục: Tổng hợp





