Mời các em cùng tìm hiểu Z là tập hợp số gì? Z là gì trong toán học? trong bài viết dưới đây.
Z là tập hợp số gì?
Trong toán học, Z là ký hiệu của tập hợp số nguyên. Tập hợp số nguyên chỉ ra các số nguyên là miền xác định nguyên duy nhất mà các phần tử dương của nó được sắp thứ tự tốt và các thứ tự đó được bảo toàn dưới phép cộng. Tương tự như các tập hợp số khác, tập hợp Z cũng là một tập hợp vô hạn.
Ví dụ: -10; -9; -8; 100 ; 0
Xem thêm:
Tập hợp Z+ và Z-
Số nguyên được chia thành 2 trường phái là số nguyên dương và số nguyên âm. Sự phân chia này không chỉ có ý nghĩa về hình thức mà còn có ý nghĩa đại số vô cùng to lớn. Số nguyên dương được kí hiệu Z+, số nguyên âm kí hiệu là Z-. Đây là những kí hiệu không chính thống do mỗi quốc gia, mỗi nền giáo dục khác nhau qui định.
Ví dụ về tập hợp Z+: 1, 2, 3, 4, 5…
Ví dụ về tập hợp Z-: -10; -11; -8; -7…
Lưu ý rằng: Số 0 chẳng thuộc Z+ và cũng chẳng thuộc Z- mà là thuộc Z!
Số nguyên là gì?
– Số nguyên là một trong những khái niệm cơ bản nhất của toán học. Số nguyên bao gồm các số nguyên dương và các số đối của chúng là số nguyên âm. Ngoài ra số nguyên còn bao gồm số 0. Đây là số duy nhất nằm giữa và là ranh giới phân biệt giữa hai đầu âm và dương.
– Nếu phát biểu theo đúng khái niệm toán học: Các số nguyên là miền nguyên bao gồm các số được sắp xếp theo một thứ tự duy nhất. Các phần tử dương của nó được sắp xếp theo một thứ tự logic với quy luật được bảo toàn bởi phép cộng. Phát biểu đơn giản và dễ hiểu hơn thì số nguyên chính là những số có thể biểu thị mà không cần sử dụng tới thành phần phân số.
Số nguyên
– Tập hợp số nguyên được ký hiệu là Z. Ký hiệu này là viết tắt của từ Zahl có nghĩa là chữ số trong tiếng Đức.
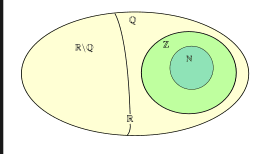
– Đây cũng là tập hợp con của hai tập hợp lớn hơn là tập hợp số hữu tỉ Q và số thực R. Đồng thời cũng là tập hợp mẹ của tập hợp số tự nhiên N.
– Tập hợp số nguyên có tính chất giống như tập hợp số tự nhiên, tập hợp số Z là vô hạn nhưng đếm được.
– Số nguyên là tập hợp bao gồm các số: Số không, số nguyên dương và số nguyên âm
+ Tập hợp số nguyên Z có thể được chia thành 2 tập hợp con là Z+ và Z-. Trong đó:
Z+ là tập hợp các nguyên dương lớn hơn 0
Z- là tập hợp các số nguyên âm nhỏ hơn 0
Một lưu ý là số 0 chỉ nằm trong tập hợp Z, không nằm trong hai tập con Z+ và Z-
Tính chất của tập số nguyên
Các số nguyên thuộc tập Z sẽ có những tính chất cơ bản sau đây:
– Không có khái niệm số nguyên lớn nhất và số nguyên nhỏ nhất. Khái niệm lớn nhất và nhỏ nhất chỉ mang tính chất tương đối và phụ thuộc vào điều kiện trong từng trường hợp.
– Số nguyên dương nhỏ nhất là 1. Số nguyên âm lớn nhất là -1.
– Số nguyên Z bao gồm vô số tập con hữu hạn. Những tập con đó sẽ có số nguyên nhỏ nhất và lớn nhất xác định.
– Không tồn tại một số nguyên nào nằm giữa hai số nguyên liên tiếp.
Biểu diễn số nguyên trên trục số
– Số nguyên âm có thể được biểu diễn trên tia đối của tia đối số đó, gọi là trục số. Điểm 0 được gọi là điểm gốc của trục số. Trục số có thể được vẽ theo hương ngang (nằm) hoặc hướng dọc (đứng)
– Khi vẽ trục số ngang, chiều từ dưới lên trên được gọi là chiều dương (cũng được đánh dấu bằng mũi tên), chiều từ trên cuống dưới gọi là chiều âm.
– Điểm biểu diễn số nguyên a trên trục số được gọi là điểm a.
=> Như vậy một trục số là một đường thẳng trên đó đã chọn điểm 0 gọi là điểm gốc, thường chọn chiều từ trái qua phải làm chiều dương và một đơn vị độ dài, mỗi số tự nhiên (hay số nguyên dương) được biểu diễn bởi một điểm ở bên phải điểm 0, mỗi số nguyên âm được biểu diễn bởi một điểm nằm ở bên trái điểm 0
Số đối
– Hai số đối nhau khi chúng cách đều điểm 0 và nằm ở hai phía của điểm 0 trên trục số. Để viết số đối của một số nguyên dương chỉ cần viết dấu “-” trước số đó và ngược lại với số nguyên âm.
So sánh hai số nguyên
Khi biểu diễn trên trục số (nằm ngang) điểm a nằm bên trái điểm b thì số nguyên a bé hơn số nguyên b. Như vậy:
+ Mọi số nguyên dương đều lớn hơn số 0
+ Mọi số âm đều bé hơn số 0 và mọi số nguyên bé hơn 0 đều là số âm
+ Mỗi số âm đều bé hơn mọi số dương.
Các bài toán sử dụng tập hợp số nguyên
Trong toán học, các dạng bài tập về số nguyên thường rất đa dạng. Nhưng loại tập hợp này thường chỉ được ra điều kiện trong một bài toán khó. Hoặc ở các chương trình nhỏ hơn chẳng hạn toán lớp 6, số nguyên lại được sử dụng như một bài toán thực thụ:

Tính hợp lý các biểu thức số nguyên sau
A = (-37) + 14 + 26 + 37
B= (-24) + 6 + 10 + 24
C = 15 + 23 + (-25) + (-23)
D = 60 + 33 + (-50) + (-33)
E = (-16) + (-209) + (-14) + 209
F = (-12) + (-13) + 36 + (-11)
G = -16 + 24 + 16 – 34
H = 25 + 37 – 48 – 25 – 37
I = 2575 + 37 – 2576 – 29
J = 34 + 35 + 36 + 37 – 14 – 15 – 16 – 17
Vậy là chúng ta vừa tìm hiểu xong tập hợp Z hay còn gọi là tập hợp số nguyên. Nếu còn thắc mắc gì về tập hợp số trên, bạn đọc vui lòng để lại bình luận bên dưới bài viết
Đăng bởi: Thcs-thptlongphu.edu.vn
Chuyên mục: Tổng hợp





