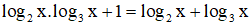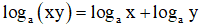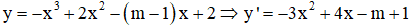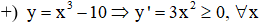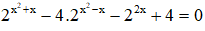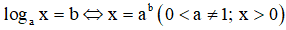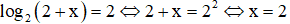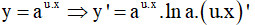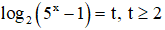Cùng tìm hiểu một số Đề thi học kì 1 môn Toán lớp 12 năm 2022 – 2023.
Đề thi học kì 1 môn Toán lớp 12 – Đề số 1
Câu 1. Đường thẳng nào cho dưới đây là tiệm cận ngang của đồ thị hàm số ![]()
A. y = -2
B. y = -1
C. x = 2
D. y = 2
Câu 2. Cho hàm số f(x) = x2lnx. Tính f'(e)
A. 3e
B. 2e
C. e
D. 2 + e
Câu 3. Viết công thức tính V của khối cầu có bán kính r.

Câu 4. Thể tích khối chóp tứ giác đều có tất cả các cạnh bằng 6 gần bằng số nào sau đây nhất?
A. 48
B. 46
C. 52
D. 51
Câu 5. Tìm tập xác định D của hàm số y = ln(x2 – 3x)
A. D = (0;3)
B. D = [0;3]
C. D = (-∞;0)∪(3;+∞)
D. D = (-∞;0)∪[3;+∞)
Câu 6. Cho hình chóp tam giác đều có cạnh bên là b và chiều cao là h (b > h). Tính thể tích của khối chóp đó.

Câu 7. Cho hàm số y = x3 – mx + 1 (với m là tham số). Tìm tất cả các giá trị của m để đồ thị hàm số cắt trục hoành tại 3 điểm phân biệt.

Câu 8. Nếu tăng chiều cao một khối chóp lên 2 lần và giảm diện tích đáy đi 6 lần thì thể tích khối chóp đó tăng hay giảm bao nhiêu lần?
A. Giảm 12 lần.
B. Tăng 3 lần.
C. Giảm 3 lần.
D. Không tăng, không giảm.
Câu 9. Cho hàm số y = f(x) có bảng biến thiên như sau:

Tìm tất cả các giá trị của tham số m để phương trình f(x) = m có ba nghiệm thực phân biệt.
A. m ∈ (-1;+∞)
B. m ∈ (-∞;3)
C. m ∈ (-1;3)
D. m ∈ [-1;3]
Câu 10. Cho hàm số y = f(x) có bảng biến thiên như hình bên. Mệnh đề nào sau đây đúng?

A. Hàm số có điểm cực tiểu bằng 0.
B. Hàm số có điểm cực đại bằng 5.
C. Hàm số có điểm cực tiểu bằng -1.
D. Hàm số có điểm cực tiểu bằng 1.
Câu 11. Cho a là số thực dương khác 1. Mệnh đều nào dưới đây đúng với mọi số dương x, y

Câu 12. Cho hàm số ![]() có đồ thị (C). Đồ thị (C) có bao nhiêu đường tiệm cận?
có đồ thị (C). Đồ thị (C) có bao nhiêu đường tiệm cận?
A. 4
B. 3
C. 1
D. 2
Câu 13. Tính thể tích khối hộp chữ nhật ABCD.A’B’C’D có AB = 3, AD = 4, AA’ = 5
A. V = 12
B. V = 60
C. V = 10
D. V = 20
Câu 14. Cho hàm số ![]() . Biết đồ thị (C) có hai tiếp tuyến cùng vuông góc với đường thẳng d: y = x. Gọi h là khoảng cách giữa hai tiếp tuyến đó. Tính h.
. Biết đồ thị (C) có hai tiếp tuyến cùng vuông góc với đường thẳng d: y = x. Gọi h là khoảng cách giữa hai tiếp tuyến đó. Tính h.

Câu 15. Cho hình chóp tứ giác đều có cạnh đáy bằng a và biết diện tích xung quanh gấp đôi diện tích đáy. Tính thể tích của khối chóp.

Câu 16. Cho khối tứ diện ABCD, M là trung điểm của AB. Mặt phẳng (MCD) chia khối tứ diện ABCD thành hai khối đa diện nào?
A. Hai khối lăng trụ tam giác.
B. Hai khối chóp tứ giác.
C. Một khối lăng trụ tam giác và một khối tứ diện
D. Hai khối tứ diện.
Câu 17. Tìm số giao điểm của đồ thị hàm số y = (x – 1)(x2 – 2x) với trục hoành.
A. 1
B. 2
C. 0
D. 3
Câu 18. Cho hàm số y = x3 + 3x2 – 9x + 1. Mệnh đề nào dưới đây đúng?
A. Hàm số nghịch biến trên khoảng (-3;1)
B. Hàm số đồng biến trên khoảng (-3;1)
C. Hàm số nghịch biến trên khoảng (1;+∞)
D. Hàm số nghịch biến trên khoảng (-∞;-3)
Câu 19. Cho a > 0. Hãy viết biểu thức  dưới dạng lũy thừa với số mũ hữu tỉ?
dưới dạng lũy thừa với số mũ hữu tỉ?

Câu 20. Tìm giá trị nhỏ nhất của hàm số y = x3 – 3x2 – 9x + 2 trên đoạn [0;4]

Câu 21. Một hình trụ có bán kính đáy r = 5cm, chiều cao h = 7cm. Tính diện tích xung quanh của hình trụ.

Câu 22. Đường cong ở hình bên là đồ thị của một trong bốn hàm số dưới đây. Hàm số đó là hàm số nào?


Câu 23. Cho tứ diện ABCD có DA vuông góc với (ABC) và AD = a, AC = 2a; cạnh BC vuông góc với cạnh AB. Tính bán kính r của mặt cầu ngoại tiếp tứ diện ABCD.

Câu 24. Cho khối chóp S.ABCD có đáy là hình chữ nhật cạnh AB = 2a, AD = a. Hình chiếu của đỉnh S lên đáy là trung điểm của AB, cạnh bên SC tạo với đáy một góc 450. Tính thể tích V của khối chóp đã cho.

Câu 25. Cho khối chóp S.ABC có SA, SB, SC đôi một vuông góc với nhau và SA = a, SB = b, SC = c. Tính thể tích khối chóp S.ABC.

Câu 26. Gọi S là tập nghiệm của phương trình 2(2x – 1) – 5.2(x – 1) + 3 = 0. Tìm S.
A. S = {1; log23 }
B. S = {0; log23 }
C. S = {1; log32 }
D. S = {1}
Câu 27. Đồ thị hàm số nào dưới đây đi qua điểm M(2;-1)

Câu 28. Viết công thức diện tích xung quanh Sxq của hình nón tròn xoay có độ dài đường sinh l và bán kính đường tròn đáy r.

Câu 29. Cho hàm số ![]() . Phương trình tiếp tuyến tại điểm M(2;5) của đồ thị hàm số trên là:
. Phương trình tiếp tuyến tại điểm M(2;5) của đồ thị hàm số trên là:
A. y = 3x – 11
B. y = -3x + 11
C. y = -3x – 11
D. y = 3x + 11
Câu 30. Tìm tập xác định D của hàm số ![]()

Câu 31. Cho đồ thị hàm số (C): y = x3 – 3x. Mệnh đề nào dưới đây sai?
A. Đồ thị (C) nhận gốc tọa độ O làm tâm đối xứng.
B. Đồ thị (C) cắt trục tung tại 1 điểm.
C. Đồ thị (C) nhận trục Oy làm trục đối xứng.
D. Đồ thị (C) cắt trục hoành tại 3 điểm phân biệt.
Câu 32. Tính đạo hàm của hàm số y = 3x

Câu 33. Cho một hình đa diện. Tìm khẳng định sai trong các khẳng định sau:
A. Mỗi cạnh là cạnh chung của ít nhất ba mặt.
B. Mỗi mặt có ít nhất ba cạnh.
C. Mỗi đỉnh là đỉnh chung của ít nhất ba mặt.
D. Mỗi đỉnh là đỉnh chung của ít nhất ba cạnh.
Câu 34. Cho hình hộp chữ nhật ABCD.A’B’C’D’ có tâm I. Gọi V, V1 lần lượt là thể tích của khối hộp ABCD.A’B’C’D’ và khối chóp I.ABCD. Tính tỉ số ![]()

Câu 35. Bảng sau là bảng biến thiên của một trong bốn hàm số dưới đây. Hàm số đó là hàm số nào?


Câu 36. Tính tổng lập phương các nghiệm của phương trình:
A. 125
B. 35
C. 13
D. 5
Câu 37. Tìm giá trị lớn nhất của hàm số ![]() trên đoạn [1;5]
trên đoạn [1;5]

Câu 38. Tìm tất cả các giá trị thực của tham số m để hàm số y = -x3 + 2x2 – (m – 1)x + 2 nghịch biến trên khoảng (-∞;+∞)

Câu 39. Cho hàm số ![]() . Gọi M là giá trị lớn nhất và m là giá trị nhỏ nhất của hàm số trên đoạn [-5;-1]. Tính M + m
. Gọi M là giá trị lớn nhất và m là giá trị nhỏ nhất của hàm số trên đoạn [-5;-1]. Tính M + m

Câu 40. Cho lăng trụ đứng ABC.A1B1C1 có đáy ABC là tam giác vuông cân tại C, 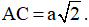

Câu 41. Trong các hàm số sau, hàm số nào đồng biến trên R?

Câu 42. Tìm điểm cực đại của đồ thị hàm số ![]()

Câu 43. Đặt a = log345. Mệnh đề nào dưới đây đúng?

Câu 44. Tính ![]()
A. 0
B. 1
C. 2017
D. +∞
Câu 45. Tìm giá trị yCT cực tiểu của hàm số y = x4 – 4x2 + 3

Câu 46. Tìm nghiệm của phương trình log2(2x – 1) = 3

Câu 47. Ông A gửi vào ngân hàng 100 triệu đồng theo hình thức lãi suất kép. Lãi suất ngân hàng là 8% trên năm và không thay đổi qua các năm ông gửi tiền. Sau 5 năm ông cần tiền sửa nhà, ông đã rút toàn bộ số tiền và sử dụng một nửa số tiền đó vào công việc, số còn lại ông tiếp tục gửi ngân hàng và với hình thức như trên. Hỏi sau 10 năm ông A đã thu được số tiền lãi là bao nhiêu? (đơn vị tính là triệu đồng).
A. ≈ 79,412
B. ≈ 80,412
C. ≈ 81,412
D. ≈ 100,412
Câu 48. Cho hàm số f(x) có đạo hàm f'(x) = (x + 1)2(x – 3). Mệnh đề nào dưới đây đúng?
A. Hàm số đạt cực đại tại x = 3
B. Hàm số đạt cực tiểu tại x = 3
C. Hàm số đạt cực tiểu tại x = -1
D. Hàm số đạt cực đại tại x = -1
Câu 49. Đồ thị hàm số  có tiệm cận đứng x = a và tiệm cận ngang y = b. Tính giá trị T = 2a – b
có tiệm cận đứng x = a và tiệm cận ngang y = b. Tính giá trị T = 2a – b
A. T = -4
B. T = -8
C. T = -1
D. T = -6
Câu 50. Hàm số nào sau đây đồng biến trên khoảng (-∞;+∞)

Đáp án & Hướng dẫn giải:

Câu 1. Đáp án D
Phương pháp:
Nếu ![]() là TCN của đồ thị hàm số.
là TCN của đồ thị hàm số.
Cách giải:
![]() Đồ thị hàm số
Đồ thị hàm số ![]() có tiệm cận ngang là: y = 2
có tiệm cận ngang là: y = 2
Câu 2. Đáp án A
Phương pháp:
Sử dụng công thức tính đạo hàm của một tích (f.g)’ = f’.g + f.g’
Cách giải:
Ta có:

Câu 3. Đáp án A
Phương pháp:
Sử dụng công thức tính thể tích khối cầu.
Cách giải:
Công thức tính V của khối cầu có bán kính r: ![]()
Câu 4. Đáp án D

Phương pháp:
Sử dụng công thức tính thể tích chóp ![]()
Cách giải:

Câu 5. Đáp án C
Phương pháp:
Hàm số y = logaf(x) (0 < a ≠ 1) xác định khi và chỉ khi ⇔ f(x) > 0
Cách giải:

Câu 6. Đáp án A

Phương pháp:
+) Gọi G là trọng tâm tam giác ABC ⇒ SG ⊥(ABC)
+) Tính diện tích tam giác đều ABC theo b và h.
+) Sử dụng công thức tính thể tích khối chóp ![]()
Cách giải:
Gọi G là trọng tâm tam giác ABC ⇒ SG ⊥(ABC)
Tam giác SCG vuông tại ![]()

Câu 7. Đáp án B
Phương pháp:
+) Xác định m để phương trình hoành độ giao điểm có 3 nghiệm phân biệt.
+) Cô lập m, sử dụng phương pháp hàm số.
Cách giải:
Phương trình hoành độ giao điểm của đồ thị hàm số y = x3 – mx + 1 và trục hoành là: x3 – mx + 1 = 0
⇔ x3 – mx + 1 = 0 ⇔ mx = x3 + 1(*)
+) x = 0:(*) ⇔ m.0 = 1: vô lý Phương trình (*) không có nghiệm x = 0 với mọi m
![]()


Số nghiệm của phương trình (**) là số giao điểm của đồ thị hàm số ![]() và đường thẳng y = m song song với trục hoành.
và đường thẳng y = m song song với trục hoành.
Để phương trình ban đầu có 3 nghiệm phân biệt ⇔ (**) có 3 nghiệm phân biệt khác 0 
Câu 8. Đáp án C
Phương pháp:
Thể tích khối chóp ![]()
Cách giải:
Thể tích khối chóp ban đầu: ![]()
Theo đề bài, ta có: ![]()
![]() Thể tích khối chóp đó giảm 3 lần.
Thể tích khối chóp đó giảm 3 lần.
Câu 9. Đáp án C
Phương pháp:
Số nghiệm của phương trình f(x) = m bằng số giao điểm của đồ thị hàm số y = f(x) và đường thẳng y = m
Cách giải:
Số nghiệm của phương trình f(x) = m(*) bằng số giao điểm của đồ thị hàm số y = f(x) và đường thẳng y = m
⇒ Để (*) có 3 nghiệm thực phân biệt thì m ∈ (-1;3)
Câu 10. Đáp án D
Phương pháp:
Nếu f'(x) đổi dấu khi qua điểm x = x0 ⇒ x = x0 là điểm cực trị của hàm số.
Cách giải:
Tại x = 1, f'(x) đổi dấu từ âm sang dương ⇒ Hàm số có điểm cực tiểu bằng 1.
Câu 11. Đáp án A
Phương pháp:
Sử dụng công thức tính logarit của 1 tích.
Cách giải:
Câu 12. Đáp án A
* Định nghĩa tiệm cận ngang của đồ thị hàm số y = f(x)
Nếu ![]() là TCN của đồ thị hàm số.
là TCN của đồ thị hàm số.
* Định nghĩa tiệm cận đứng của đồ thị hàm số y = f(x)
Nếu ![]() thì x = a là TCĐ của đồ thị hàm số.
thì x = a là TCĐ của đồ thị hàm số.
Cách giải:

Đồ thị hàm số (C) có tất cả 4 đường tiệm cận.
Câu 13. Đáp án B
Phương pháp:
Thể tích khối hộp chữ nhật: V = abc
Cách giải:
Thể tích khối hộp chữ nhật ABCD.A’B’C’D’: V = 3.4.5 = 60
Câu 14. Đáp án D
Phương pháp:
Phương trình tiếp tuyến của đồ thị hàm số y = f(x) tại điểm M(x0; y0) là: y = f'(x0).(x – x0) + y0
Cách giải:
![]()
Tiếp tuyến của (C) vuông góc với đường thẳng d: y = x nên tiếp tuyến có hệ số góc k = -1

Ta có:

Câu 15. Đáp án D.

Phương pháp:
+) Gọi b là độ dài cạnh bên, sử dụng giả thiết diện tích xung quanh gấp đôi diện tích đáy biểu diễn b theo a.
+) Gọi O = AC ∩ BD ⇒ SO ⊥ (ABCD)
![]()
Cách giải:
Gọi b là độ dài cạnh bên, I là trung điểm của BC ⇒ SI ⊥ BC
Tam giác SIB vuông tại 


Câu 16. Đáp án D

Cách giải:
Mặt phẳng (MCD) chia khối tứ diện ABCD thành hai khối đa diện là: A.MCD và M.BCD
Câu 17. Đáp án D
Phương pháp:
Giải phương trình hoành độ giao điểm.
Cách giải:

Vậy đồ thị hàm số y = (x – 1)(x2 – 2x) cắt trục hoành tại 3 điểm.
Câu 18. Đáp án A

Phương pháp:
Tính y’, xét dấu y’ và tìm các khoảng đơn điệu của hàm số.
Cách giải:

Hàm số nghịch biến trên khoảng (-3;1)
Câu 19. Đáp án B
Phương pháp:
Sử dụng các công thức: ![]()
Cách giải:

Câu 20. Đáp án C
Phương pháp:
Phương pháp tìm GTLN, GTNN của hàm số y = f(x) trên [a;b]
+) Bước 1: Tính y’, giải phương trình y’ = 0 ⇒ xi ∈ [a;b]
+) Bước 2: Tính các giá trị f(a); f(b); f(xi)
+) Bước 3: 
Cách giải:

Hàm số đã cho liên tục trên đoạn [0;4] có y(0) = 2, y(3) = -25, y(4) = -18 ![]()
Câu 21. Đáp án B
Phương pháp:
Diện tích xung quanh của hình trụ: Sxq = 2πrh
Cách giải:
Diện tích xung quanh của hình trụ: Sxq = 2πrh = 2π.5.7 = 70π(cm2)
Câu 22. Đáp án C
Phương pháp:
Nhận biết đồ thị hàm số bậc bốn trùng phương, hàm số bậc ba.
Cách giải:
Quan sát đồ thị hàm số, ta thấy: đây không phải đồ thị hàm số bậc 3 ⇒ Loại bỏ phương án B và D
Đồ thị hàm số cắt trục tung tại điểm có tung độ dương ⇒ Chọn phương án C.
Câu 23. Đáp án D

Phương pháp:
+) Xác định tâm mặt cầu ngoại tiếp khối tứ diện là điểm cách đều tất cả các đỉnh của tứ diện.
+) Áp dụng định lí Pytago tính bán kính mặt cầu ngoại tiếp tứ diện.
Cách giải:
Tam giác ABC vuông tại B, M là trung điểm của AC ⇒ M là tâm đường tròn ngoại tiếp tam giác ABC
Gọi I là trung điểm của CD ⇒ IC = ID(1)
Ta có: IM là đường trung bình của tam giác ACD ⇒ IM // AD
Mà AD ⊥ (ABC) ⇒ IM ⊥ (ABC)
Do đó, IM là trục đường tròn ngoại tiếp tam giác ABC
⇒ IA = IB = IC(2)
Từ (1), (2) ⇒ IA = IB = IC = ID ⇒ I là tâm mặt cầu ngoại tiếp tứ diện ABCD, bán kính mặt cầu:

Câu 24. Đáp án A

Phương pháp:
+) Xác định góc giữa SC và mặt đáy là góc giữa SC và hình chiếu của nó trên (ABCD).
+) Áp dụng định lí Pytago tính SM.
![]()
Cách giải:
Gọi M là trung điểm của AB ⇒ SM ⊥ (ABCD)

Câu 25. Đáp án A

Phương pháp:
Thể tích khối chóp vuông ![]()
Cách giải:
S.ABC có SA, SB, SC đôi một vuông góc với nhau
⇒ S.ABC là tứ diện vuông tại đỉnh ![]()
Câu 26. Đáp án A
Phương pháp:
Đặt ẩn phụ, đưa về phương trình bậc hai một ẩn. Giải phương trình và suy ra ẩn t.
Cách giải:

Câu 27. Đáp án C
Phương pháp:
Thay tọa độ điểm M và các hàm số.
Cách giải:
Ta có: ![]() luôn đúng ⇒ M(2;-1) nằm trên đồ thị hàm số
luôn đúng ⇒ M(2;-1) nằm trên đồ thị hàm số ![]()
Câu 28. Đáp án C
Cách giải:
Công thức diện tích xung quanh Sxq của hình nón: Sxq = πrl
Câu 29. Đáp án B
Phương pháp:
Phương trình tiếp tuyến của đồ thị hàm số y = f(x) tại điểm M(x0; y0) là y = f'(x0).(x – x0) + y0
Cách giải:

Câu 30. Đáp án D

Câu 31. Đáp án C
Phương pháp:
Sử dụng tính chất:
+) Hàm số lẻ nhận gốc tọa độ làm tâm đối xứng.
+) Hàm số chẵn nhận trục Oy làm trục đối xứng.
Cách giải:

⇒ Hàm số y = x3 – 3x là hàm lẻ ⇒ Đồ thị (C) nhận điểm O làm tâm đối xứng ⇒ A đúng
+) Cho x = 0 ⇒ y = 0 ⇒ Đồ thị hàm số cắt trục tung tại điểm duy nhất O(0;0) ⇒ B đúng
+) Xét phương trình hoành độ giao điểm  Đồ thị (C) cắt trục hoành tại 3 điểm phân biệt ⇒ D đúng.
Đồ thị (C) cắt trục hoành tại 3 điểm phân biệt ⇒ D đúng.
Câu 32. Đáp án C
Phương pháp: (ax)’ = ax.lna
Cách giải: y = 3x ⇒ y’ = 3xln3
Câu 33. Đáp án A
Cách giải:
Khẳng định sai là: Mỗi cạnh là cạnh chung của ít nhất ba mặt.
Câu 34. Đáp án A

Phương pháp:
Xác định tỉ số chiều cao và tỉ số diện tích đáy của chóp I.ABCD và khối hộp ABCD.A’B’C’D’.
Cách giải:

Câu 35. Đáp án C
Phương pháp:
Dựa vào TCĐ và TCN của đồ thị hàm số.
Cách giải:
Đồ thị hàm số có TCĐ là x = 2 và TCN là ![]()
Câu 36. Đáp án B
Phương pháp:
Đưa phương trình về dạng tích sau đó giải phương trình logarit cơ bản.
Cách giải:
ĐKXĐ: x > 0

Tổng lập phương các nghiệm của phương trình là: 33 + 23 = 35
Câu 37. Đáp án B
Phương pháp:
Phương pháp tìm GTLN, GTNN của hàm số y = f(x) trên [a;b]
+) Bước 1: Tính y’, giải phương trình y’ = 0 ⇒ xi ∈ [a;b]
+) Bước 2: Tính các giá trị f(a); f(b); f(xi)
+) Bước 3: 
Cách giải:

Hàm số đã cho liên tục trên đoạn [1;5] có:
![]()
Câu 38. Đáp án B
Phương pháp:
Hàm số y = f(x) nghịch biến trên (-∞;+∞) khi và chỉ khi f'(x) ≤ 0, ∀ x ∈ (-∞;+∞), f'(x) = 0 tại hữu hạn điểm.
Cách giải:
Hàm số đã cho nghịch biến trên khoảng (-∞;+∞) ⇔ y’ ≤ 0, ∀x 

Câu 39. Đáp án B
Phương pháp:
Phương pháp tìm GTLN, GTNN của hàm số y = f(x) trên [a;b]
+) Bước 1: Tính y’, giải phương trình y’ = 0 ⇒ xi ∈ [a;b]
+) Bước 2: Tính các giá trị f(a); f(b); f(xi)
+) Bước 3: 
Cách giải:

Câu 40. Đáp án D

Phương pháp:
Thể tích khối lăng trụ: V = Sh
Cách giải:
ABC là tam giác vuông cân tại C, 

Câu 41. Đáp án B
Phương pháp:
Xét hàm số y = ax, 0 < a ≠ 1
+) a > 1: Hàm số đồng biến trên R.
+) 0 < a < 1: Hàm số nghịch biến trên R.
Cách giải:
Hàm số nào đồng biến trên R là: 
Câu 42. Đáp án D
Phương pháp:
Nếu  là điểm cực đại của hàm số.
là điểm cực đại của hàm số.
Cách giải:

Câu 43. Đáp án D
Phương pháp:
Sử dụng công thức đổi cơ số: ![]()
Cách giải:

Câu 44. Đáp án C

Câu 45. Đáp án D
Phương pháp:
Nếu  là điểm cực tiểu của hàm số.
là điểm cực tiểu của hàm số.
Cách giải:

Câu 46. Đáp án C
Phương pháp:

Câu 47. Đáp án C
Phương pháp:
Công thức lãi kép, không kỳ hạn: An = M(1 + r%)n
Với: An là số tiền nhận được sau tháng thứ n,
M là số tiền gửi ban đầu,
n là thời gian gửi tiền (tháng),
r là lãi suất định kì (%).
Cách giải:
Số tiền ông A rút ra sau 5 năm đầu là: 100.1 + 8%5 ≈ 146,933 (triệu đồng)
Số tiền ông A tiếp tục gửi là: 146,933:2 ≈ 73,466 (triệu đồng)
Số tiền ông A nhận được sau 5 năm còn lại là: 73,466.1 + 8%5 ≈ 107,946 (triệu đồng)
Sau 10 năm ông A đã thu được số tiền lãi là: 107,946 – 73,466 + 146,933-100 ≈ 81,412 (triệu đồng)
Câu 48. Đáp án B
Phương pháp:
Nếu f'(x) đổi dấu khi qua điểm x = x0 ⇒ x = x0 là điểm cực trị của hàm số.
Cách giải:
f'(x) đổi dấu từ – sang + tại x = 3 ⇒ Hàm số đạt cực tiểu tại x = 3
Câu 49. Đáp án A
* Định nghĩa tiệm cận ngang của đồ thị hàm số y = f(x)
Nếu ![]() là TCN của đồ thị hàm số.
là TCN của đồ thị hàm số.
* Định nghĩa tiệm cận đứng của đồ thị hàm số y = f(x)
Nếu ![]() thì x = a là TCĐ của đồ thị hàm số.
thì x = a là TCĐ của đồ thị hàm số.
Cách giải:

Câu 50. Đáp án B
Phương pháp:
Xét từng hàm số, giải bất phương trình y’ ≥ 0
Cách giải:
y = x3 + 1 ⇒ y’ = 3x2 ≥ 0, ∀ x ∈ R, y’ = 0 tại điểm duy nhất x = 0
⇒ Hàm số y = x3 + 1 đồng biến trên khoảng (-∞;+∞)
Đề thi học kì 1 môn Toán lớp 12 – Đề số 2
Câu 1. Cho hàm số ![]() . Khẳng định nào sau đây đúng?
. Khẳng định nào sau đây đúng?
A. Hàm số đồng biến trên khoảng (2;+∞)
B. Hàm số nghịch biến trên khoảng 
C. Hàm số nghịch biến trên khoảng (2;+∞)
D. Hàm số đồng biến trên khoảng 
Câu 2. Cho lăng trụ tứ giác đều có cạnh bằng a và cạnh bên bằng 2a. Diện tích xung quanh của hình lăng trụ đã cho bằng
A. 10a2
B. 9a2
C. 8a2
D. 4a2
Câu 3. Thể tích của khối cầu tiếp xúc với tất cả các cạnh của hình lập phương cạnh 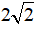

Câu 4. Đồ thị hàm số ![]() có bao nhiêu tiệm cận?
có bao nhiêu tiệm cận?
A. 3
B. 1
C. 2
D. 4
Câu 5. Cho  . Khẳng định nào sau đây đúng?
. Khẳng định nào sau đây đúng?

Câu 6. Số giao điểm của đồ thị hàm số y = x3 – 4x + 1 và đường thẳng y = x + 1 bằng:
A. 1
B. 2
C. 3
D. 4
Câu 7. Bất phương trình  có nghiệm là
có nghiệm là
A. x > -4
B. x < -4
C. x ≥ -4
D. x ≤ -4
Câu 8. Cho hàm số y = f(x) có đồ thị như hình vẽ. Khẳng định nào sau đây đúng?

A. Hàm số nghịch biến trên khoảng (-1;+∞)
B. Hàm số đồng biến trên khoảng (1;+∞)
C. Hàm số đồng biến trên khoảng (-1;+∞)
D. Hàm số nghịch biến trên khoảng (-1;0)
Câu 9. Tập nghiệm S của bất phương trình  là
là

Câu 10. Cho biểu thức  . Khẳng định nào sau đây đúng?
. Khẳng định nào sau đây đúng?
A. A = 4 + 2a
B. A = 4 – 2a
C. A = 1 + 2a
D. A = 1 – 2a
Câu 11. Số giao điểm của đồ thị hàm số ![]() với trục hoành là
với trục hoành là
A. 3
B. 4
C. 1
D. 5
Câu 12. Một hình đa diện có ít nhất bao nhiêu đỉnh?
A. 6
B. 3
C. 5
D. 4
Câu 13. Tính đạo hàm của hàm số y = xe + ex

Câu 14. Hàm số y = x3 – 3x có giá trị cực đại bằng
A. 2
B. –2
C. 1
D. –1
Câu 15. Cho hàm số  . Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số trên đoạn
. Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số trên đoạn  . Tính tích M.m.
. Tính tích M.m.

Câu 16. Diện tích toàn phần của hình trụ có thiết diện qua trục là hình vuông cạnh a bằng

Câu 17. Cho khối chóp S.ABC có ba cạnh SA, SB, SC cùng độ dài bằng a và vuông góc với nhau từng đôi một. Thể tích của khối chóp S.ABC bằng

Câu 18. Cho hàm số y = f(x) liên tục trên R và có bảng biến thiên như sau:

Khẳng định nào sau đây đúng?
A. Hàm số y = f(x) nghịch biến trên một đoạn có độ dài bằng 1.
B. Giá trị lớn nhất của hàm số y = f(x) trên R bằng 0.
C. Hàm số y = f(x) chỉ có một cực trị.
D. Giá trị nhỏ nhất của hàm số y = f(x) trên R bằng -1.
Câu 19. Thể tích của khối bát diện đều cạnh a bằng

Câu 20. Trong không gian, cho hai điểm phân biệt A, B cố định. Xét điểm M di động luôn nhìn đoạn AB dưới một góc vuông. Hỏi điểm M thuộc mặt nào trong các mặt sau?
A. Mặt trụ.
B. Mặt nón.
C. Mặt cầu.
D. Mặt phẳng.
Câu 21. Cho phương trình log5(x2 + x + 1) = 1. Khẳng định nào sau đây đúng?
A. Phương trình có một nghiệm bằng 0 và một nghiệm âm.
B. Phương trình vô nghiệm.
C. Phương trình có hai nghiệm âm.
D. Phương trình có hai nghiệm trái dấu.
Câu 22. Phương trình  có bao nhiêu nghiệm thực?
có bao nhiêu nghiệm thực?
A. 1
B. 3
C. 2
D. Vô số
Câu 23. Hàm số ![]() nghịch biến trên khoảng
nghịch biến trên khoảng

Câu 24. Cho hàm số y = log2x. Xét các phát biểu
(1) Hàm số y = log2x đồng biến trên khoảng (0;+∞) .
(2) Hàm số y = log2x có một điểm cực tiểu.
(3) Đồ thị hàm số y = log2x có tiệm cận.
Số phát biểu đúng là
A. 0
B. 1
C. 3
D. 2
Câu 25. Cho hàm số y = f(x) có đồ thị như hình vẽ. Hàm số y = f(x) là:


Câu 26. Các tiệm cận của đồ thị hàm số ![]() là
là

Câu 27. Cắt một khối nón bởi mặt phẳng đi qua trục của nó, ta được một tam giác vuông cân có diện tích bằng 8. Khẳng định nào sau đây sai ?
A. Khối nón có diện tích đáy bằng 8π
B. Khối nón có diện tích xung quanh bằng
C. Khối nón có độ dài đường sinh bằng 4.
D. Khối nón có thể tích bằng ![]()
Câu 28. Tổng tất cả các nghiệm của phương trình 4x – 3.2x + 1 + 8 = 0
A. 1 + log23
B. 1 – log23
C. 3
D. 6
Câu 29. Hàm số nào sau đây có giá trị nhỏ nhất trên đoạn [0;2] bằng –2?

Câu 30. Khối mười hai mặt đều là khối đa diện đều loại

A. {3;4}
B. {4;3}
C. {5;3}
D. {3;5}
Câu 31. Cho mặt nón có chiều cao h = 6, bán kính đáy r = 3. Hình lập phương ABCD.A’B’C’D’ đặt trong mặt nón sao cho trục của mặt nón đi qua tâm hai đáy của hình lập phương, một đáy của hình lập phương nằm trong cùng một mặt phẳng đáy của hình trụ, các đỉnh của đáy còn lại thuộc các đường sinh của hình nón. Độ dài đường chéo của hình lập phương bằng


Câu 32. Bạn Nam làm một cái máng thoát nước mưa, mặt cắt là hình thang cân có độ dài hai cạnh bên và cạnh đáy đều bằng 20cm, thành máng nghiêng với mặt đất một góc φ(0° < φ < 90°). Bạn Nam phải nghiêng thành máng một góc trong khoảng nào sau đây để lượng mưa thoát được là nhiều nhất?

Câu 33. Theo thống kê dân số năm 2017, mật độ dân số của Việt Nam là 308 người/km2 và mức tăng trưởng dân số là năm. Với mức tăng trưởng như vậy, tới năm bao nhiêu mật độ dân số Việt Nam đạt 340 người 1,03%/km2
A. Năm 2028
B. Năm 2027
C. Năm 2026
D. Năm 2025
Câu 34. Cho các hàm số y = logax, y = logbx và y = cx (với a, b, c là các số dương khác 1) có đồ thị như hình vẽ. Khẳng định nào sau đây đúng?

A. c > b > a
B. c > a > b
C. a > b > c
D. b > a > c
Câu 35. Biết rằng phương trình ![]() có nghiệm khi và chỉ khi m ∈ [a;b], với m là tham số. Giá trị của b – a bằng
có nghiệm khi và chỉ khi m ∈ [a;b], với m là tham số. Giá trị của b – a bằng
![]()
Câu 36. Cho phương trình ![]() . Tìm tất cả các giá trị của tham số thực m để phương trình đã cho có 4 nghiệm phân biệt.
. Tìm tất cả các giá trị của tham số thực m để phương trình đã cho có 4 nghiệm phân biệt.
A. m < 2 log23
B. m > -2 log23 m
C. m ∈ ∅
D. 2 log23 < m <2 log23
Câu 37. Cho hình chóp S.ABCD có đáy là hình thang vuông tại A và B, AB = BC = 2, AD = 4; mặt bên SAD nằm trong mặt phẳng vuông góc với đáy và có diện tích bằng 6. Thể tích khối S.BCD bằng
A. 6
B. 18
C. 2
D. 1
Câu 38. Cho tứ diện ABCD có AB = x thay đổi, tất cả các cạnh còn lại có độ dài a. Tính khoảng cách giữa hai đường thẳng AB và CD trong trường hợp thể tích của khối tứ diện ABCD lớn nhất.

Câu 39. Cho hình chóp tam giác đều S.ABC với ![]() . Diện tích của mặt cầu có tâm A và tiếp xúc với mặt phẳng (SBC) bằng
. Diện tích của mặt cầu có tâm A và tiếp xúc với mặt phẳng (SBC) bằng

Câu 40. Đồ thị của hàm số nào sau đây có ba tiệm cận?

Câu 41. Một khối gỗ hình hộp chữ nhật có chiều dài, chiều rộng và chiều cao lần lượt là 30cm, 20cm và 30cm (như hình vẽ). Một con kiến xuất phát từ điểm A muốn tới điểm B thì quãng đường ngắn nhất nó phải đi là bao nhiêu cm?


Câu 42. Cho hàm số ![]() có giá trị cực đại y1 và giá trị cực tiểu y2. Giá trị của S = y1 – y2 bằng
có giá trị cực đại y1 và giá trị cực tiểu y2. Giá trị của S = y1 – y2 bằng
A. S = 8
B. S = 0
C. S = -2
D. S = -8
Câu 43. Cho hàm số y = f(x) và y = g(x) có đồ thị lần lượt như hình vẽ

Đồ thị hàm số y = f(x).g(x) là đồ thị nào dưới đây?

Câu 44. Phương trình ![]() có nghiệm trong khoảng nào sau đây?
có nghiệm trong khoảng nào sau đây?

Câu 45. Tìm tất cả các giá trị thực của tham số m để hàm số y = x3 – 3x + m có giá trị cực đại và giá trị cực tiểu trái dấu.
A. m ∈ {-2;2}
B. m < -2 hoặc m > 2
C. -2 < m < 2
D. m ∈ R
Câu 46. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh 2a, SA ⊥ (ABCD) và SA = a. Gọi E là trung điểm của cạnh AB. Diện tích mặt cầu ngoại tiếp hình chóp bằng .SBCE
A. 14πa2
B. 11πa2
C. 8πa2
D. 12πa2
Câu 47. Gọi giá trị nhỏ nhất, giá trị lớn nhất của hàm số y = lnx trên đoạn  lần lượt là m và M. Tích M.m bằng
lần lượt là m và M. Tích M.m bằng

Câu 48. Phương trình 3.9x – 7.6x + 2.4x = 0 có hai nghiệm x1, x2. Tổng x1 + x2 bằng

Câu 49. Phương trình |x|3 – 3x2 – m2 = 0 (với m là tham số thực) có nhiều nhất bao nhiêu nghiệm phân biệt
A. 4 nghiệm.
B. 3 nghiệm.
C. 2 nghiệm.
D. 6 nghiệm.
Câu 50. Cho hàm số ![]() có đồ thị (C). Có bao nhiêu giá trị thực của tham số m để đường thẳng y = 2x + m cắt đồ thị (C) tại hai điểm phân biệt mà tiếp tuyến của t(C) ại hai điểm đó song song với nhau?
có đồ thị (C). Có bao nhiêu giá trị thực của tham số m để đường thẳng y = 2x + m cắt đồ thị (C) tại hai điểm phân biệt mà tiếp tuyến của t(C) ại hai điểm đó song song với nhau?
A. 0
B. 2
C. Vô số
D. 1
Đáp án & Hướng dẫn giải:

Câu 1. Đáp án C
Phương pháp:
* Phương pháp xét sự đồng biến, nghịch biến của các hàm số:
– Bước 1: Tìm tập xác định, tính f'(x)
– Bước 2: Tìm các điểm tại đó f'(x) = 0 hoặc f'(x) không xác định
– Bước 3: Sắp xếp các điểm đó theo thứ tự tăng dần và lập bảng biến thiên
– Bước 4: Kết luận về các khoảng đồng biến, nghịch biến của hàm số.
Cách giải:
Tập xác định: D = R{2}

Câu 2. Đáp án C
Phương pháp:
Diện tích xung quanh của hình hộp chữ nhật: Sxq = 2(a + b)h (trong đó, a, b là chiều dài, chiều rộng của đáy, h là chiều cao)
Diện tích xung quanh của lăng trụ tứ giác đều: Sxq = 4ah trong đó, a là độ dài cạnh đáy, h là chiều cao) .
Cách giải:
Diện tích xung quanh của hình lăng trụ đã cho bằng: 4.a.2a = 8a2
Câu 3. Đáp án C
Phương pháp:
Thể tích khối cầu có bán kính R là ![]()
Cách giải:
Bán kính của khối cầu tiếp xúc với tất cả các cạnh của hình lập phương cạnh 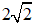

Câu 4. Đáp án A
Phương pháp:
* Định nghĩa tiệm cận ngang của đồ thị hàm số y = f(x)
Nếu ![]() là TCN của đồ thị hàm số.
là TCN của đồ thị hàm số.
* Định nghĩa tiệm cận đứng của đồ thị hàm số y = f(x)
Nếu ![]() thì x = a là TCĐ của đồ thị hàm số.
thì x = a là TCĐ của đồ thị hàm số.
Cách giải:
Tập xác định: D = R{-2;2}
 Đồ thị hàm số có 1 tiệm cận ngang là y = 0
Đồ thị hàm số có 1 tiệm cận ngang là y = 0

Đồ thị có 2 đường tiệm cận đứng là x = -2 và x = 2.
Câu 5. Đáp án A

Câu 6. Đáp án C
Phương pháp:
Số giao điểm của hai đồ thị hàm số bằng số nghiệm của phương trình hoành độ giao điểm.
Cách giải:
Phương trình hoành độ giao điểm của đồ thị hàm số y = x3 – 4x + 1 và đường thẳng y = x + 1 là:

Số giao điểm của hai đồ thị hàm số bằng số nghiệm của phương trình hoành độ giao điểm và bằng 3.
Câu 7. Đáp án C
Phương pháp:
Xét hàm số có dạng y = ax, a > 0, a ≠ 1
+ Nếu 0 < a < 1: hàm số nghịch biến trên (-∞;+∞)
+ Nếu a > 1: hàm số đồng biến trên (-∞;+∞)

Câu 8. Đáp án B
Cách giải:
Hàm số đồng biến trên khoảng (1;+∞)
Câu 9. Đáp án D
Phương pháp:

Kết hợp điều kiện xác định, suy ra, bất phương trình có tập nghiệm ![]()
Câu 10. Đáp án B

Câu 11. Đáp án A
Số giao điểm của hai đồ thị hàm số bằng số nghiệm của phương trình hoành độ giao điểm.
Cách giải:
Phương trình hoành độ giao điểm của đồ thị hàm số với trục hoành là:

Vậy, đồ thị hàm số ![]() giao với trục hoành tại 3 điểm.
giao với trục hoành tại 3 điểm.
Câu 12. Đáp án D
Cách giải:
Một hình đa diện có ít nhất 4 đỉnh.
Câu 13. Đáp án B

Câu 14. Đáp án A
Phương pháp:
– Tìm TXĐ
– Tính đạo hàm
– Lập bảng xét dấu y’
– Xác định điểm cực đại và tính giá trị cực đại.
Cách giải:
Tập xác định: D = R
y = x3 – 3x ⇒ y’ = 3x2 – 3
y’= 0 ⇔ x = ±1
Bảng xét dấu y’

Hàm số đạt cực đại tại x = -1 và giá trị cực đại yCĐ = 2
Câu 15. Đáp án C
Phương pháp:
– Tìm TXĐ
– Tính y’
– Lập bảng biến thiên của hàm số trên đoạn 
– Xác định giá trị lớn nhất và giá trị nhỏ nhất của hàm số
– Tính tích M.m.
Cách giải:
TXĐ: D = R{1}


Giá trị nhỏ nhất ![]() , giá trị lớn nhất
, giá trị lớn nhất ![]()
Câu 16. Đáp án B
Phương pháp:
Diện tích xung quanh của hình trụ: Sxq = 2πRh
Diện tích toàn phần của hình trụ: Stp = Sxq + S2đáy = 2πRh + 2πR2
Cách giải:
Thiết diện qua trục là hình vuông cạnh a nên hình trụ đã cho có chiều cao h = a, bán kính đáy ![]()
Diện tích toàn phần của hình trụ là:

Câu 17. Đáp án A
Phương pháp:
Khối chóp S.ABC có ba cạnh SA, SB, SC vuông góc với nhau từng đôi một là một tứ diện vuông tại đỉnh S
Thể tích của tứ diện vuông có độ dài ba cạnh góc vuông bằng a, b, c là: ![]()
Cách giải:
Thể tích của khối chóp S.ABC bằng: ![]()
Câu 18. Đáp án A
Phương pháp:
Dựa vào BBT và đánh giá từng đáp án.
Cách giải:
Hàm số y = f(x) nghịch biến trên đoạn [0;1], đoạn này có độ dài bằng 1 ⇒ Phương án A đúng.
Hàm số không có GTLN, GTNN trên R ⇒ B và D sai.
Hàm số đạt cực trị tại 2 điểm ⇒ C sai
Câu 19. Đáp án D

Phương pháp:
Khối bát diện đều được ghép bởi hai khối chóp tứ giác bằng nhau, do vậy, ta tính thể tích bát diện bằng cách tính 2 lần thể tích khối chóp tứ giác đều.
Cách giải:
Thể tích của một khối chóp là:

Câu 20. Đáp án C
Cách giải:
M di động luôn nhìn đoạn AB dưới một góc vuông ⇒ M thuộc mặt cầu có một đường kính là AB.
Câu 21. Đáp án D

Do a.c = 1.(-4) < 0 nên phương trình trên có 2 nghiệm trái dấu.
Câu 22. Đáp án A
Phương pháp:
Đưa về cùng số mũ.
Cách giải:
![]()
Phương trình đã cho chỉ có 1 nghiệm thực duy nhất.
Câu 23. Đáp án A
Phương pháp:
– Tìm TXĐ
– Tính y’
– Lập bảng xét dấu y’
– Đánh giá khoảng nghịch biến.
Cách giải:

Bảng xét dấu y’:

Hàm số ![]() nghịch biến trên khoảng (-∞;0)
nghịch biến trên khoảng (-∞;0)
Câu 24. Đáp án D
Phương pháp:
Đánh giá từng đáp án.
Cách giải:
(1) Hàm số y = log2x đồng biến trên khoảng (0;+∞): đúng, do 2 > 1
(2) Hàm số y = log2x có một điểm cực tiểu: sai, hàm số y = log2x luôn đồng biến trên (0;+∞)
(3) Đồ thị hàm số y = log2x có tiệm cận: đúng, tiệm cận đó là đường x = 0
Số phát biểu đúng là 2.
Câu 25. Đáp án B
Phương pháp:
Phân biệt dạng đồ thị của các hàm số : bậc nhất trên bậc nhất, bậc ba, bậc bốn trùng phương.
Cách giải:
Quan sát đồ thị hàm số, ta thấy, đồ thị hàm số không thể là đồ thị của hàm bậc nhất trên bậc nhất và bậc bốn trùng phương. Do đó, loại phương án A và D.
Còn lại, phương án B và C là các hàm số bậc ba.
Quan sát đồ thị ta thấy, khi x → +∞ thì y → +∞ nên ta chọn B (a = 1 > 0)
Câu 26. Đáp án D
Phương pháp:
Đồ thị hàm số bậc nhất trên bậc nhất ![]() , (a,c ≠ 0, ad – bc ≠ 0) có tiệm cận đứng là
, (a,c ≠ 0, ad – bc ≠ 0) có tiệm cận đứng là ![]() , tiệm cận ngang là
, tiệm cận ngang là ![]()
Cách giải:
Các tiệm cận của đồ thị hàm số ![]() là x = 1, y = 2
là x = 1, y = 2
Câu 27. Đáp án B

Phương pháp:
Diện tích hình tròn bán kính R: S = πR2
Diện tích xung quanh của khối nón: Sxq = πRl
Thể tích khối nón: ![]()
Cách giải:
Theo đề bài, ta có tam giác SAB vuông cân tại S và SΔSAB = 8
Ta có:

Câu 28. Đáp án C
Phương pháp:
Đặt 2x = t, (t > 0). Giải phương trình tìm , sau đó tìm và tổng các nghiệm.
Cách giải:
Đặt 2x = t, (t > 0). Phương trình trở thành:

Tổng hai nghiệm của phương trình đã cho là: 1 + 2 = 3
Câu 29. Đáp án C
Phương pháp:
Sử dụng phương pháp tìm GTNN, GTLN của hàm số.
Cách giải:
⇒ Hàm số đồng biến trên ![]()
![]()
⇒ Hàm số đồng biến trên ![]()

⇒ Hàm số đồng biến trên 
⇒ Hàm số đồng biến trên ![]()
Câu 30. Đáp án C
Cách giải:
Khối mười hai mặt đều là khối đa diện đều loại {5;3}
Câu 31. Đáp án A
Phương pháp:
Cắt khối hình bởi mặt phẳng đi qua trục
Tính độ dài x cạnh của hình lập phương
Tính độ dài đường chéo của hình lập phương:
Cách giải:

Xét mặt cắt qua trục có SH = h = 6, HA = HB = r = 3
Gọi độ dài cạnh của hình vuông là x.

Câu 32. Đáp án D
Phương pháp:
Tính thể tích của khối lăng trụ đứng, có đáy là hình thang cân mà hai cạnh bên bằng đáy bé và bằng 20cm.
Thể tích lớn nhất khi diện tích của hình thang cân lớn nhất.
Cách giải:
Thể tích nước lớn nhất khi diện tích của hình thang cân lớn nhất

Gọi độ dài đường cao là h. Khi đó, AE = BF = h,

Bảng xét dấu:


Câu 33. Đáp án B
Phương pháp:
Công thức: An = M(1 + r%)n
Với: An là mật độ dân số ở năm thứ n,
M là mật độ dân số ban đầu,
n là thời gian (năm),
r là mức tăng trưởng dân số.
Cách giải:
Ta có:

⇒ Ta cần 10 năm để đạt mật độ dân số như vậy
⇒ Đến năm 2027 mật độ dân số nước ta đạt đến con số đó.
Câu 34. Đáp án D
Cách giải:
Ta thấy, hai hàm số y = logax, y = logbx đều đồng biến trên (0;+∞) ⇒ a, b > 1
Lấy x0 > 0 bất kì, ta thấy logax0 > logbx0 ⇒ a < b ⇒ 1 < a < b
Hàm số y = cx nghịch biến trên R ⇒ c < 1 ⇒ c < a < b
Câu 35. Đáp án A


Câu 36. Đáp án A

Phương pháp:
Cô lập m, đưa về dạng f(x) = m
Số nghiệm của phương trình là số giao điểm của đồ thị hàm số y = f(x) và đường thẳng y = m
Cách giải:
Điều kiện: x ≠ 2, x ≠ -4

Số nghiệm của phương trình đã cho bằng số giao điểm của đồ thị hàm số y = |x2 + 2x – 8| và đường thẳng y = 2m
Quan sát đồ thị hàm số bên, ta thấy, để đồ thị hàm số y = |x2 + 2x – 8| cắt đường thẳng y = 2m tại 4 điểm phân biệt thì 0 < 2m < 9 ⇔ m < log29 ⇔ m < 2 log23
Câu 37. Đáp án C

Phương pháp:
Thể tích khối chóp: ![]()
Cách giải:
Kẻ SH vuông góc AB (H thuộc AB). Do mặt bên SAD nằm trong mặt phẳng vuông góc với đáy ⇒ SH ⊥ (ABCD)

Câu 38. Đáp án B

Cách giải:
Gọi M là trung điểm của CD. Kẻ AH vuông góc mặt phẳng (BCD) (H thuộc (BCD)) ⇒ H ∈ BM, AH ⊥ HM
VABCD lớn nhất khi và chỉ khi AH có độ dài lớn nhất, tức là khi H trùng M
Hai tam giác ACD, BCD đều, cạnh a, có đường cao AM, BM bằng ![]()
Tam giác ABM vuông cân tại A, lấy N là trung điểm của AB ⇒ MN ⊥ AB
Mà MN ⊂ (AMB) ⊥ CD ⇒ MN ⊥ CD ⇒ MN là đoạn vuông góc chung của AB và CD
Khoảng cách giữa hai đường thẳng AB và CD là: 
Câu 39. Đáp án B

Phương pháp:
Mặt cầu tâm A tiếp xúc với (SBC) có bán kính R = d(A;(SBC))
Diện tích mặt cầu: Smc = 4πR2
Cách giải:
Gọi M, N lần lượt là trung điểm của AB, BC; O là giao điểm của AN và CM. Kẻ AH ⊥ SN (H ∈ SN)
Tam giác ABC đều, tâm O 
Tam giác SAO vuông tại O ![]()
Tam giác SBC cân tại N ⇒ SN ⊥ BC ⇒ Tam giác SNC vuông tại N

Tam giác AHN đồng dạng tam giác SON 
Diện tích mặt cầu: 
Câu 40. Đáp án A
Phương pháp:
Tìm số đường tiệm cận của từng đồ thị hàm số
Cách giải:
Đồ thị hàm số  có 3 đường tiệm cận là x = 0, x = 2, y = 0
có 3 đường tiệm cận là x = 0, x = 2, y = 0
Đồ thị hàm số ![]() có 1 đường tiệm cận là x = 1, x = -1
có 1 đường tiệm cận là x = 1, x = -1
Đồ thị hàm số ![]() có 2 đường tiệm cận là x = 0, y = 0
có 2 đường tiệm cận là x = 0, y = 0
Đồ thị hàm số ![]() có 2 đường tiệm cận là x = 2, y = 0
có 2 đường tiệm cận là x = 2, y = 0
Câu 41. Đáp án B
Phương pháp:
Trải tất cả các mặt của hình hộp chữ nhật ra cùng một mặt phẳng.
Cách giải:


Để đến được B, đầu tiên con kiến phải đi trên một trong các mặt bên và đi đến một trong các cạnh bên: NP, PE, QE, MQ, MF, NF
* Giả sử con kiến đi đến I trên cạnh MF sau đó tới B, khi đó để độ dài quãng đường là ngắn nhất thì A, I, B thẳng hàng:
Độ dài ![]()
* Giả sử con kiến đi đến I trên cạnh NF sau đó tới B, khi đó để độ dài quãng đường là ngắn nhất thì A, I, B thẳng hàng:
Độ dài ![]()
* Giả sử con kiến đi đến I trên cạnh PF sau đó tới B, khi đó để độ dài quãng đường là ngắn nhất thì A, I, B thẳng hàng:
Độ dài ![]()
Vậy, quãng đường ngắn nhất con kiến đi là
Câu 42. Đáp án D
Phương pháp:
Khảo sát, tìm giá trị cực đại và cực tiểu của hàm số. Từ đó tính S.
Cách giải:

Bảng xét dấu y’:

Hàm số đạt cực đại tại x = -1, giá trị cực đại y1 = -4, đạt cực tiểu tại x = 1, giá trị cực tiểu y2 = 4
S = y1 – y2 = – 4 – 4 = -8
Câu 43. Đáp án C.

Cách giải:
Đặt y = f(x).g(x) = h(x). Khi đó:
h(0) = f(0).g(0) = 0.0 = 0
h(1) = f(1).g(1) = 1.(-1) = -1
Do đó, ta chọn phương án C
Câu 44. Đáp án B
Phương pháp:
Sử dụng tính đơn điệu của hàm số.
Cách giải:

Phương trình đã cho tương đương:

Câu 45. Đáp án C
Phương pháp:
+) Tính y’, giải phương trình y’ = 0 ⇒ các cực trị của hàm số.
+) Tính các giá trị cực trị của hàm số và yCT.yCĐ < 0
Cách giải:

Giá trị cực đại và giá trị cực tiểu trái dấu ⇒ (-2 + m)(2 + m) < 0 ⇔ -2 < m < 2
Câu 46. Đáp án A

Phương pháp:
Sử dụng phương pháp tọa độ hóa.
Cách giải:
Gắn hệ trục tọa độ như hình vẽ.
Trong đó, B(2a;0;0), C(2a;2a;0), E(a;0;0), S(0;0;a)
Gọi I(x0;y0;z0) là tâm của mặt cầu ngoại tiếp hình chóp S.BEC. Khi đó, IS2 = IB2 = IC2 = IE2

Câu 47. Đáp án A
Phương pháp:
– Tìm TXĐ
– Tìm nghiệm và điểm không xác định của y’
– Tính các giá trị tại 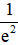
– Tính tích M.m.
Cách giải:
TXĐ: D = (0;+∞)

Câu 48. Đáp án D
Phương pháp:
Chia cả hai vế cho 4x, đặt  . Giải phương trình tìm t, từ đó tìm x và tổng x1 + x2
. Giải phương trình tìm t, từ đó tìm x và tổng x1 + x2
Cách giải:

Câu 49. Đáp án B
Phương pháp:
Số nghiệm của phương trình |x3| – 3x2 – m2 = 0 bằng số giao điểm của đồ thị hàm số y = |x|3 – 3x2 và đường thẳng y = m2
Phác họa đồ thị hàm số , từ đó nhận xét số giao điểm trên.
Cách giải:
Số nghiệm của phương trình |x3| – 3x2 – m2 = 0 bằng số giao điểm của đồ thị hàm số y = |x|3 – 3x2 và đường thẳng y = m2
Từ đồ thị hàm số y = x3 – 3x2

Ta vẽ được đồ thị hàm số y = |x|3 – 3x2 như sau:

Do m2 ≥ 0,∀m nên đồ thị hàm số y = |x|3 – 3x2 cắt đường thẳng y = m2 tại nhiều nhất 3 điểm.
Câu 50. Đáp án D
Cách giải:
Xét phương trình hoành độ giao điểm của (C) và đường thẳng y = 2x + m:

Dễ dàng kiểm tra được x = 2 không phải nghiệm của phương trình (*) với mọi m
Để phương trình (*) có 2 nghiệm phân biệt x1, x2 thì Δ > 0 ⇔ (m – 6)2 + 8(2m + 3) > 0 ⇔ m2 + 4m + 60 > 0, luôn đúng

Tiếp tuyến của (C) tại hai điểm giao song song với nhau

Vậy, có 1 giá trị thực của tham số m thỏa mãn yêu cầu đề bài.
Đề thi học kì 1 môn Toán lớp 12 – Đề số 3
Câu 1. Đường cong ở hình bên là đồ thị của một trong bốn hàm số dưới đây. Hàm số đó là hàm số nào?


Câu 2. Cho hàm số ![]() có đồ thị như hình vẽ bên. Tìm khẳng định đúng trong các khẳng định sau
có đồ thị như hình vẽ bên. Tìm khẳng định đúng trong các khẳng định sau

A. a > 0, b < 0, c > 0
B. a > 0, b > 0, c < 0
C. a > 0, b < 0, c < 0
D. a < 0, b > 0, c > 0
Câu 3. Cho hàm số ![]() . Mệnh đề nào dưới đây đúng?
. Mệnh đề nào dưới đây đúng?
A. Đường thẳng y = 2 là đường tiệm cận đứng của đồ thị hàm số.
B. Hàm số không có giá trị nhỏ nhất.
C. Hàm số có một điểm cực trị.
D. Hàm số nghịch biến trên R.
Câu 4. Tìm số giao điểm của đồ thị hàm số ![]() và đường thẳng y = 2x
và đường thẳng y = 2x
A. 1
B. 0
C. 3
D. 2
Câu 5. Cho hình chóp S.BACD có đáy ABCD là hình chữ nhật, 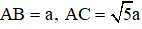
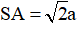

Câu 6. Tìm giá trị lớn nhất M của hàm số y = x4 – 2x2 + 1 trên đoạn [0;2]
A. M = 9
B. M = 10
C. M = 1
D. M = 0
Câu 7. Cho log23 = a. Tính T = log3624 theo a.

Câu 8. Một hình nón có chiều cao bằng a và thiết diện qua trục của hình nón đó là tam giác vuông. Tính theo a diện tích xung quanh của hình nón đó.

Câu 9. Giá trị nhỏ nhất, giá trị lớn nhất của hàm số y = x – lnx trên đoạn  lần lượt là
lần lượt là

Câu 10. Tập xác định của hàm số y = (x + 1)-2 là
A. (-1;+∞)
B. [-1;+∞)
C. R
D. R{-1}
Câu 11. Cho hình lăng trụ đứng ABC.A’B’C’ có đáy ABC là tam giác cân tại A, ![]() . Tính theo a thể tích V của khối lăng trụ ABC.A’B’C’.
. Tính theo a thể tích V của khối lăng trụ ABC.A’B’C’.

Câu 12. Cho hình hộp chữ nhật ABCD.A’B’C’D’ có 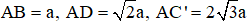

Câu 13. Trong không gian với hệ tọa độ Oxyz, cho hai vectơ ![]() . Khẳng định nào đúng?
. Khẳng định nào đúng?

Câu 14. Trong không gian với hệ tọa độ Oxyz, cho các điểm A(2;1;-1), B(3;3;1), C(4;5;3). Khẳng định nào đúng?
A. AB ⊥ AC
B. A, B, C thẳng hàng.
C. AB = AC
D. O, A, B, C là 4 đỉnh của một hình tứ diện.
Câu 15. Trong không gian với hệ tọa độ Oxyz, cho tam giác OAB có A(-1;-1;0), B(1;0;0). Tính độ dài đường cao kẻ từ O của tam giác OAB.

Câu 16. Hàm số nào sau đây không đồng biến trên khoảng (-∞;+∞)

Câu 17. Với a, b, c là các số thực dương, a và c khác 1 và α ≠ 0. Mệnh đề nào dưới đây sai?

Câu 18. Cho hình chóp đều S.ABCD có tất cả các cạnh bằng nhau. Khẳng định nào đúng?
A. Tâm mặt cầu ngoại tiếp hình chóp trùng với đỉnh S.
B. Tâm mặt cầu ngoại tiếp hình chóp là tâm của mặt đáy ABCD.
C. Tâm mặt cầu ngoại tiếp hình chóp là trung điểm của đoạn thẳng nối S với tâm của mặt đáy ABCD.
D. Tâm mặt cầu ngoại tiếp hình chóp là trọng tâm tam giác SAC.
Câu 19. Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a, ![]() . Cạnh bên
. Cạnh bên 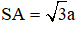

Câu 20. Tìm mệnh đề đúng trong các mệnh đề sau
A. Đồ thị các hàm số y = ax và ![]() đối xứng nhau qua trục tung.
đối xứng nhau qua trục tung.
B. Hàm số y = ax, 0 < a ≠ 1 đồng biến trên R
C. Hàm số y = ax, a > 1 nghịch biến trên R
D. Đồ thị hàm số y = ax, 0 < a ≠ 1 luôn đi qua điểm có tọa độ (a;1)
Câu 21. Đường tiệm cận ngang của đồ thị hàm số ![]() là
là
A. x = 2
B. y = -2
C. x = -2
D. y = 2
Câu 22. Ông An gửi 100 triệu đồng vào ngân hàng với hình thức lãi kép, kỳ hạn 1 năm với lãi suất 8%/năm. Sau 5 năm ông rút toàn bộ tiền và dùng một nửa để sửa nhà, số tiền còn lại ông tiếp tục gửi vào ngân hàng với kỳ hạn và lãi suất như lần trước. Số tiền lãi mà ông An nhận được sau 10 năm gửi gần nhất với giá trị nào sau đây?
A. 34,480 triệu.
B. 81,413 triệu.
C. 107,946 triệu.
D. 46,933 triệu.
Câu 23. Đạo hàm của hàm số y = xlnx trên khoảng (0;+∞) là

Câu 24. Cho biểu thức ![]() , với x > 0. Mệnh đề nào dưới đây đúng?
, với x > 0. Mệnh đề nào dưới đây đúng?

Câu 25. Cho hàm số y = f(x) có bảng biến thiên như sau

Mệnh đề nào dưới đây là sai?
A. Giá trị cực đại của hàm số là y = 2
B. Điểm cực đại của đồ thị hàm số là (-1;2)
C. Hàm số không đạt cực tiểu tại điểm x = 2
D. Hàm số đạt cực đại tại điểm x = -1
Câu 26. Trong các mệnh đề sau, mệnh đề nào sai?

Câu 27. Số đường tiệm cận ngang của đồ thị hàm số
A. 0
B. 1
C. 3
D. 2
Câu 28. Trong không gian với hệ tọa độ Oxyz, cho các vectơ ![]() . Khẳng định nào đúng?
. Khẳng định nào đúng?

Câu 29. Tìm tập nghiệm S của bất phương trình 

Câu 30. Trong không gian với hệ tọa độ Oxyz, cho các điểm A(1;2;3), B(2;1;5), C(2;4;2). Góc giữa hai đường thẳng AB và AC bằng
A. 60°
B. 150°
C. 30°
D. 120°
Câu 31. Tập xác định của hàm số y = ln(-x2 + 5x – 6)
A. (2;3)
B. R{2;3}
C. R(2;3)
D. [2;3]
Câu 32. Tìm số nghiệm nguyên của bất phương trình
A. 6
B. 5
C. 4
D. 3
Câu 33. Một xưởng in có 8 máy in, mỗi máy in được 4000 bản in khổ giấy A4 trong một giờ. Chi phí để bảo trì, vận hành một máy mỗi lần in là 50 nghìn đồng. Chi phí in ấn của n máy chạy trong một giờ là 20(3n + 5) nghìn đồng. Hỏi nếu in 50 000 bản in khổ A4 thì phải sử dụng bao nhiêu máy để thu được lãi nhiều nhất?
A. 6 máy
B. 7 máy
C. 5 máy
D. 4 máy
Câu 34. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, mặt bên SAB là tam giác cân tại S và nằm trong mặt phẳng vuông góc với (ABCD). Biết rằng côsin của góc giữa (SCD) và (ABCD) bằng ![]() . Tính theo a thể tích V của khối chóp S.ABCD.
. Tính theo a thể tích V của khối chóp S.ABCD.

Câu 35. Cho hàm số y = f(x) có đạo hàm là ![]() và f(1) = 1. Giá trị f(5)
và f(1) = 1. Giá trị f(5)
A. 1 + ln3
B. ln2
C. 1 + ln2
D. ln3
Câu 36. Tìm nguyên hàm của hàm số ![]()

Câu 37. Giá trị của tham số m để phương trình 4x – m.2(x + 1) + 2m = 0 có 2 nghiệm x1, x2 thỏa mãn x1 + x2 = 3 là
A. m = 2
B. m = 3
C. m = 1
D. m = 4
Câu 38. Cho hàm số ![]() . Gọi F(x) là một nguyên hàm của f(x). Khẳng định nào sau là sai?
. Gọi F(x) là một nguyên hàm của f(x). Khẳng định nào sau là sai?

Câu 39. Tìm tất cả các giá trị của tham số thực m để hàm số y = -x3 – 2x2 + mx + 1 đạt cực tiểu tại điểm x = -1
A. m < -1
B. m ≠ -1
C. m = -1
D. m > -1
Câu 40. Cho hàm số f(x) = ax4 + bx2 + c với a > 0, c > 2017, a + b + c < 2017. Số cực trị của hàm số y = |f(x) – 2017| là
A. 1
B. 5
C. 3
D. 7
Câu 41. Số nghiệm của phương trình  là
là
A. 2
B. 0
C. 1
D. 3
Câu 42. Nguyên hàm của f(x) = xcosx là
A. F(x) = -xsinx – cosx + C
B. F(x) = xsinx + cosx + C
C. F(x) = xsinx – cosx + C
D. F(x) = -xsinx + cosx + C
Câu 43. Cho hàm số có đạo hàm f'(x) = x2(x – 1)(x – 4)2. Khi đó số cực trị của hàm số y = f(x2) là
A. 3
B. 4
C. 5
D. 2
Câu 44. Cho hình trụ có bán kính đáy bằng r, chiều cao bằng h. Khẳng định nào sai?
A. Diện tích toàn phần của hình trụ bằng 2πrh + πr2 + πh2
B. Thiết diện qua trục của hình trụ là hình chữ nhật có diện tích 2rh.
C. Thể tích của khối trụ bằng πr2h
D. Khoảng cách giữa trục của hình trụ và đường sinh của hình trụ bằng r.
Câu 45. Cho hàm số liên tục trên khoảng (a;b) và x0 ∈ (a;b). Có bao nhiêu mệnh đề đúng trong các mệnh đề sau?
(1) Hàm số đạt cực trị tại điểm x0 khi và chỉ khi f'(x0) = 0.
(2) Nếu hàm số y = f(x) có đạo hàm và có đạo hàm cấp hai tại điểm x0 thỏa mãn điều kiện f'(x0) = f”(x0 ) = 0 thì điểm x0 không phải là điểm cực trị của hàm số y = f(x).
(3) Nếu f'(x) đổi dấu khi x qua điểm x0 thì điểm x0 là điểm cực tiểu của hàm số y = f(x)
(4) Nếu hàm số y = f(x)có đạo hàm và có đạo hàm cấp hai tại điểm x0 thỏa mãn điều kiện f'(x0) = 0, f”(x0 ) > 0 thì điểm x0 là điểm cực tiểu của hàm số y = f(x).
A. 1
B. 2
C. 0
D. 3
Câu 46. Cho hình chóp S.ABCD có đáy là hình vuông, hình chiếu của S lên (ABCD) là điểm H thuộc cạnh AB thỏa mãn HB = 2HA, góc giữa SC và (ABCD) bằng 60°. Biết rằng khoảng cách từ A đến (SCD) bằng 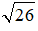

Câu 47. Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, 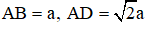

Câu 48. Cho hình nón đỉnh S, đáy là đường tròn (O; r). Một mặt phẳng đi qua đỉnh của hình nón cắt đường tròn đáy tại hai điểm A và B sao cho ![]() . Tính theo r khoảng cách từ O đến (SAB).
. Tính theo r khoảng cách từ O đến (SAB).

Câu 49. Tìm m để phương trình ![]() có 2 nghiệm phân biệt.
có 2 nghiệm phân biệt.

Câu 50. Số giá trị nguyên của tham số m để phương trình 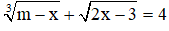
A. 7
B. 6
C. 5
D. 8
Đáp án & Hướng dẫn giải:
Bạn đang xem: 5 Đề thi học kì 1 môn Toán lớp 12 năm 2022 – 2023

Câu 1. Đáp án A
Phương pháp:
Nhận dạng đồ thị hàm số bậc ba
Cách giải:
Quan sát đồ thị hàm số ta thấy khi x → +∞ thì y → +∞ nên hệ số a > 0 ⇒ Loại phương án C và D
Mặt khác đồ thị hàm số đạt cực trị tại hai điểm: x = 0 và x = x0 > 0
Xét  Loại phương án B
Loại phương án B
Ta chọn phương án A.
Câu 2. Đáp án C
Phương pháp:
Đồ thị hàm số ![]() có hai đường tiệm cận: x = c và y = a, đồng thời cắt trục hoành tại điểm
có hai đường tiệm cận: x = c và y = a, đồng thời cắt trục hoành tại điểm 
Cách giải:
Quan sát đồ thị hàm số ta thấy: Đồ thị hàm số có tiệm cận đứng x = x0 < 0 ⇒ c < 0, đồ thị hàm số có tiệm cận ngang y = y_0 > 0 ⇒ a > 0
Đồ thị hàm số cắt trục hoành tại điểm ![]()
Mà a > 0 ⇒ b < 0
Vậy a > 0, b < 0, c < 0
Câu 3. Đáp án B
Phương pháp:
Hàm bậc nhất trên bậc nhất luôn đơn điệu trên từng khoảng xác định của nó.
Cách giải:
Hàm số bậc nhất trên bậc nhất không có giá trị nhỏ nhất.
Câu 4. Đáp án D
Phương pháp:
Số giao điểm của hai đồ thị hàm số bằng số nghiệm của phương trình hoành đồ giao điểm của hai hàm số đó.
Cách giải:
Xét phương trình hoành độ giao điểm: ![]()

⇒ Số giao điểm của hai đồ thị hàm số là 2.
Câu 5. Đáp án C

Phương pháp:
Sử dụng công thức tính thể tích khối chóp: ![]()
Với: S là diện tích của đáy,
h là chiều cao của khối chóp.
Cách giải: .
Xét tam giác vuông ABC có:

Câu 6. Đáp án A
Phương pháp:
– TXĐ
– Tính nghiệm và tìm các điểm không xác định ‘ y
– Tìm các giá trị tại x = 0, x = 2 và các điểm đã tìm ở trên (nằm trong đoạn đang xét) 0, 2 x x
– Xác định giá trị lớn nhất trong các giá trị đó.
Cách giải:
TXĐ: D = R

Câu 7. Đáp án D

Câu 8. Đáp án D

Phương pháp:
Diện tích xung quanh của khối nón: Sxq = πRl
Cách giải:
Theo đề bài, ta có tam giác SAB là tam giác vuông cân tại S, SO = a ⇒ R = OA = SO = a

Câu 9. Đáp án A
Phương pháp:
– Tìm TXĐ
– Tìm nghiệm và các điểm không xác định của y’ trên đoạn 
– Tính các giá trị tại 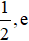
– Kết luận GTLN, GTNN của hàm số từ các giá trị trên.
Cách giải:
TXĐ: D = (0;+∞)

⇒ Giá trị nhỏ nhất, giá trị lớn nhất của hàm số lần lượt là: 1 và e – 1
Câu 10. Đáp án D
Phương pháp:
Tập xác định của hàm số y = xα:
+) Nếu α là số nguyên dương thì TXĐ: D = R
+) Nếu α là số nguyên âm hoặc bằng 0 thì TXĐ: D = R{0}
+) Nếu α là số không nguyên thì TXĐ: D = (0;+∞)
Cách giải:
Hàm số xác định ⇔ x + 1 ≠ 0 ⇔ x ≠ -1
Vây tập xác định của hàm số y = (x + 1)-2 là R{-1}
Câu 11. Đáp án D

Phương pháp:
Thể tích khối lăng trụ: V = Sh, trong đó: S là diện tích đáy, h là chiều cao.
Cách giải:

Câu 12. Đáp án C

Phương pháp:
Thể tích khối hộp chữ nhật: V = abc
Cách giải:

Câu 13. Đáp án B
Phương pháp :
Thử lần lượt từng đáp án.
Cách giải:
![]()
Câu 14. Đáp án B
Phương pháp :
Tính các vectơ 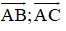
Cách giải:
A(2;1;-1), B(3;3;1), C(4;5;3) ![]() A, B, C thẳng hàng.
A, B, C thẳng hàng.
Câu 15. Đáp án A
Phương pháp:
Công thức khoảng cách từ điểm đến đường thẳng trong không gian:
 là VTCP của Δ và M là điểm bất kì thuộc
là VTCP của Δ và M là điểm bất kì thuộc
Cách giải:

Độ dài đường cao kẻ từ O của tam giác OAB bằng khoảng cách từ O đến đường thẳng AB:

Câu 16. Đáp án A
Phương pháp:
* Phương pháp xét sự đồng biến, nghịch biến của các hàm số:
– Bước 1: Tìm tập xác định, tính f'(x)
– Bước 2: Tìm các điểm tại đó f'(x) = 0 hoặc f'(x) không xác định
– Bước 3: Sắp xếp các điểm đó theo thứ tự tăng dần và lập bảng biến thiên
– Bước 4: Kết luận về các khoảng đồng biến, nghịch biến của hàm số.
Cách giải:
+) ![]() Hàm số đồng biến trên các khoảng (-∞;-2);(-2;+∞)
Hàm số đồng biến trên các khoảng (-∞;-2);(-2;+∞)
+) y = x3 + 2 ⇒ y’= 3x2 ≥ 0,∀ x∈R: Hàm số đồng biến trên R.
+) y = x + 1 ⇒ y’ = 1 > 0, ∀ x∈R: Hàm số đồng biến trên R.
+) y = x5 + x3 – 1 ⇒ y’ = 5x4 + 3x2 ≥ 0, ∀ x ∈ R; y’ = 0 ⇔ x = 0 ⇒ Hàm số đồng biến trên R.
Câu 17. Đáp án B
Phương pháp:
Sử dụng các công thức liên quan đến logarit.
Cách giải:
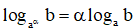
![]() )
)
Câu 18. Đáp án B

Phương pháp:
– Xác định tâm I của đáy, dựng đường (d) vuông góc với mặt đáy tại I
– Dựng mặt phẳng trung trực (P) của cạnh SA
– Xác định giao tuyến O của mặt phẳng (P) và đường thẳng (d). O chính là tâm mặt cầu ngoại tiếp hình chóp.
Cách giải:
Gọi O là tâm của đáy ⇒ OA = OB = OC = OD(1)
Do hình chóp có tất cả các cạnh đều bằng nhau nên ΔSAC = ΔBAC ⇒ OS = OA = OC(2)
Từ (1), (2) ⇒ OA = OB = OC = OD = OS ⇒ Tâm mặt cầu ngoại tiếp hình chóp là tâm của mặt đáy ABCD.
Câu 19. Đáp án B

Phương pháp:
Thể tích khối chóp: V = Sh
Cách giải:

Câu 20. Đáp án A
Phương pháp:
Dựa vào hình dáng đồ thị hàm số mũ và tính đơn điệu của hàm số mũ.
Cách giải:
Đáp án A: Ví dụ đồ thị các hàm số 

Chúng đối xứng nhau qua trục tung. Do đó đáp án A đúng.
Đáp án B và C hiển nhiên sai.
Đáp án D sai vì (a;1) thuộc đồ thị hàm số y = ax ⇔ 1 = aa không phải luôn đúng.
Câu 21. Đáp án D
Phương pháp:
Đồ thị hàm số bậc nhất trên bậc nhất ![]() có tiệm cận đứng là
có tiệm cận đứng là 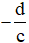
![]()
Cách giải:
Đường tiệm cận ngang của đồ thị hàm số ![]() là y = 2
là y = 2
Câu 22. Đáp án A
Phương pháp:
Công thức lãi kép, không kỳ hạn: An = M(1 + r%)n
Với:
An là số tiền nhận được sau tháng thứ n,
M là số tiền gửi ban đầu,
n là thời gian gửi tiền (tháng),
r là lãi suất định kì (%)
Cách giải:
Số tiền ông An rút lần 1 là: 100.(1 + 8%)5 = 146,9328077 (triệu đồng)
Số tiền ông An gửi lần 2 là: 146.9328077 : 2 = 73,46640384 (triệu đồng)
Số tiền ông An rút lần 2 (gửi 5 năm tiếp theo) là:
73,46640384.(1 + 8%)5 = 107,9462499 (triệu đồng)
Số tiền lãi là: 107,9462499 – 73,4660384 = 34,47984602 ≈ 34,480 (triệu đồng).
Câu 23. Đáp án D
Phương pháp: (uv)’ = u’v + uv’
Cách giải: ![]()
Câu 24. Đáp án D

Câu 25. Đáp án C
Phương pháp:
Dựa vào bảng biến thiên.
Cách giải:
Dựa vào BBT ta dễ thấy hàm số đạt cực tiểu tại điểm x = 2 nên Đáp án C sai.
Câu 26. Đáp án D
Phương pháp:

Cách giải:
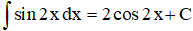
![]() )
)
Câu 27. Đáp án B
Phương pháp:
* Định nghĩa tiệm cận ngang của đồ thị hàm số y = f(x)
Nếu ![]() là tiệm cận ngang của đồ thị hàm số.
là tiệm cận ngang của đồ thị hàm số.
Cách giải:
TXĐ: D = R

Vậy, đồ thị hàm số có tất cả 1 tiệm cận ngang là đường thẳng y=0
Câu 28. Đáp án D

Cách giải:
+) 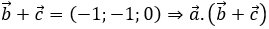
+) ![]() Đáp án B sai.
Đáp án B sai.
+) 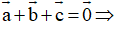
Câu 29. Đáp án C
Phương pháp:

Cách giải:

Câu 30. Đáp án A
Phương pháp:
Đường thẳng d và d’ có các VTCP lần lượt là 
Cách giải:

Câu 31. Đáp án A
Phương pháp:
Hàm số y = lnx xác định ⇔ x > 0
Cách giải:
Điều kiện xác định: -x2 + 5x – 6 > 0 ⇔ 2 < x < 3
Vậy tập xác định của hàm số y = ln(-x2 + 5x – 6) là (2;3)
Câu 32. Đáp án D
Phương pháp:
– Tìm TXĐ
– Giải bất phương trình và tìm số nghiệm nguyên.
Cách giải:
Điều kiện xác định: 

Vậy bất phương trình có 3 nghiệm nguyên.
Câu 33. Đáp án C
Cách giải:
Nhận xét: Để thu được nhiều lãi nhất thì tổng chi phí bảo trì, chi phí in ấn là ít nhất.
Gọi số máy in cần sử dụng là n (máy), n ∈ N; n ∈ (0;8)
Số giờ cần để in hết 50 000 bản in là: ![]()
Chi phí để n máy hoạt động trong 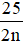

Vậy, nếu in 50 000 bản in khổ A4 thì phải sử dụng 5 máy sẽ thu được lãi nhiều nhất.
Câu 34. Đáp án B

Phương pháp:
Xác định góc giữa hai mặt phẳng (α;β)
– Tìm giao tuyến Δ của (α;β)
– Xác định 1 mặt phẳng γ ⊥ Δ
– Tìm các giao tuyến a = α∩γ, b = β ∩ γ
– Góc giữa hai mặt phẳng (α;β):(α;β) = (a;b)
Cách giải:

Gọi I, J lần lượt là trung điểm của AB, CD.
Tam giác SAB cân tại S ⇒ SI ⊥ AB
Vì mặt bên SAB nằm trong mặt phẳng vuông góc với (ABCD) nên SI ⊥ (ABCD)

Câu 35. Đáp án A
Phương pháp:

Cách giải:

Câu 36. Đáp án B

Câu 37. Đáp án D
Phương pháp:
Đặt 2x = t, t > 0. Chuyển về bài toán tìm m để phương trình bậc 2 ẩn t có 2 nghiệm t1, t2 thỏa mãn t1.t2 = 8
Cách giải:

Để phương trình (1) có 2 nghiệm x1, x2 thỏa mãn x1 + x2 = 3 thì phương trình (2) có 2 nghiệm t1,t2 thỏa mãn t1.t2 = 2x1.2x2 = 2x1 + x2 = 23 = 8

Câu 38. Đáp án C
Phương pháp: ![]()
Cách giải:

Câu 39. Đáp án C
Phương pháp:
Hàm số bậc ba y = f(x) đạt cực tiểu tại x = x0 khi và chỉ khi 
Cách giải:

Câu 40. Đáp án D
Phương pháp:
+) Xét hàm số h(x) = f(x) – 2017 = ax4 + bx2 + c – 2017
+) Tìm số điểm cực trị của hàm số h(x) bằng cách giải phương trình h'(x) = 0
+) Xác định dấu của h(0); h(1); h(-1) và vẽ đồ thị hàm số y = h(x), từ đó vẽ đồ thị hàm số y = |h(x)| và kết luận.
Cách giải:

Xét hàm số h(x) = f(x) – 2017 = ax4 + bx2 + c – 2017,
với a > 0, c > 2017, a + b + c < 2017 nên b < 0
Ta có: 
Do ![]() nên h'(x) = 0 có 3 nghiệm phân biệt
nên h'(x) = 0 có 3 nghiệm phân biệt
Ta có: h(0) = c – 2017 > 0, h(-1) = h(1) = a + b + c – 2017 < 0
⇒ h(0).(h-1) < 0, h(0).h(1) < 0
⇒ ∃ x1, x2: x1 ∈ (-1;0), x2 ∈ (0;1) mà h(x1) = h(x2) = 0
Do đó, đồ thị hàm số y = h(x) và y = |h(x)| dạng như hình vẽ bên.
Vậy, số cực trị của hàm số y = |f(x) – 2017| là 7
Câu 41. Đáp án C
Phương pháp:

Cách giải:
Điều kiện xác định: 

Vậy phương trình đã cho có 1 nghiệm là x = 1
Câu 42. Đáp án B
Phương pháp: ∫udv = uv – ∫vdu
Cách giải:
F(x) = ∫f(x).dx = ∫x.cosx.dx = ∫x.dsinx = x.sinx – ∫sinx.dx = x.sinx + cosx + C
Câu 43. Đáp án A
Phương pháp:
Tính và xét dấu của f(x2)’ từ đó tính số cực trị.
Cách giải:

Câu 44. Đáp án A
Phương pháp:
Dựa vào các công thức tính diện tích toàn phần, diện tích xung quanh và thể tích của khối trụ.
Cách giải:
Diện tích toàn phần của hình trụ bằng 2πrh + 2πr2. Do đó đáp án A sai.
Câu 45. Đáp án A
Phương pháp:
Dựa vào khái niệm cực trị và các kiến thức liên quan.
Cách giải:
(1) chỉ là điều kiện cần mà không là điều kiện đủ.
VD hàm số y = x3 có y’ = 3x2 = 0 ⇔ x = 0. Tuy nhiên x = 0 không là điểm cực trị của hàm số.
(2) sai, khi f”(x0) = 0, ta không có kết luận về điểm x0 có là cực trị của hàm số hay không.
(3) hiển nhiên sai.
Vậy (1), (2), (3): sai; (4): đúng
Câu 46. Đáp án C

Phương pháp:
+) d(A;(SCD)) = d(H;(SCD)) xác định khoảng cách từ H đến (SCD).
+) Xác định góc giữa SC và mặt đáy.
+) Đặt cạnh của hình vuông ở đáy là x, tính SH và HI theo x.
+) Sử dụng hệ thức lượng trong tam giác vuông để tìm x.
+) Tính ![]()
Cách giải:

Giả sử độ dài cạnh hình vuông ở đáy là x. Khi đó, HI = x

Thể tích khối chóp S.ABCD:

Câu 47. Đáp án C
Phương pháp:
+) Gọi I là tâm đường tròn ngoại tiếp tam giác AHC và E là trung điểm của BC.
+) Qua I dựng đường thẳng song song với SH, qua E dựng đường thẳng song song với IH, hai đường thẳng này cắt nhau tại O ⇒ O là tâm mặt cầu ngoại tiếp chóp S.AHC. O
+) Tính IH, sử dụng công thức ![]() với a, b, c là ba cạnh của tam giác AHC, S là diện tích tam giác AHC, R là bán kính đường tròn ngoại tiếp tam giác AHC.
với a, b, c là ba cạnh của tam giác AHC, S là diện tích tam giác AHC, R là bán kính đường tròn ngoại tiếp tam giác AHC.
+) Tính HE.
+) Sử dụng định lí Pytago tính OH.
Cách giải:

Kẻ HK vuông góc AB tại K, gọi I là tâm đường tròn ngoại tiếp tam giác AHC, E là trung điểm của SH.
Ta có: H là trung điểm của AB, tam giác SAB cân tại S ⇒ SH ⊥ AB
Mà SAB nằm trong mặt phẳng vuông góc với đáy ⇒ SH ⊥ (ABCD)
ΔAHK đồng dạng ΔACB (g.g)

I là tâm đường tròn ngoại tiếp tam giác AHB

Vậy, bán kính mặt cầu ngoại tiếp hình chóp S.HAC là ![]()
Câu 48. Đáp án B
Phương pháp:
+) Xác định khoảng cách từ O đến (SAB)
+) Sử dụng hệ thức lượng trong tam giác vuông để tính khoảng cách vừa xác định được.
Cách giải:
Gọi I là trung điểm của AB, kẻ OH vuông góc SI tại H.

ΔSOI vuông tại O, OH ⊥ SI ⇒ OH.SI = SO.OI 
Câu 49. Đáp án A
Phương pháp:
+) Số nghiệm của phương trình ![]() là số giao điểm của đồ thị hàm số
là số giao điểm của đồ thị hàm số
+) Vẽ hai đồ thị hàm số trên cùng hệ trục tọa độ và biện luận.
Cách giải:

Số nghiệm của phương trình ![]() là số giao điểm của đồ thị hàm số
là số giao điểm của đồ thị hàm số
Trong đó, 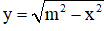
Quan sát đồ thị, ta thấy: để 2 đồ thị cắt nhau tại 2 điểm phân biệt thì bán kính của đường tròn x2 + y2 = m2 phải lớn hơn 1 
Câu 50. Đáp án B
Phương pháp:
+) Đặt 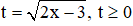
+) Thế vào phương trình, lập phương hai vế, cô lập m, đưa phương trình về dạng m = f(t)
+) Khảo sát và lập BBT của hàm số y = f(t), t ≥ 0 Biện luận để phương trình có 2 nghiệm phân biệt.
Cách giải:
Đặt ![]() . Phương trình trở thành:
. Phương trình trở thành:

Bảng biến thiên:

Để phương trình có 3 nghiệm phân biệt t ≥ 0 thì ![]() ⇒ m ∈ {8;9;10;11;12;13}
⇒ m ∈ {8;9;10;11;12;13}
⇒ Có 6 giá trị nguyên của m thỏa mãn.
Đề thi học kì 1 môn Toán lớp 12 – Đề số 4
Câu 1. Tìm khoảng nghịch biến của hàm số y = x3 + 3x2 + 2
A. (2;+∞)
B. (0;2)
C. (-2;0)
D. (-∞;2)∪(0;+∞)
Câu 2. Hình đa diện đều nào dưới đây không có tâm đối xứng?

A. Hình bát diện đều.
B. Hình lập phương.
C. Hình tứ diện đều.
D. Hình lăng trụ lục giác đều.
Câu 3. Cho tam giác đều ABC có đường cao AI. Khi tam giác ABC quay quanh trục là đường thẳng AI một góc 360° thì các cạnh của tam giác ABC sinh ra hình gì?
A. Hai hình nón.
B. Một hình nón.
C. Một mặt nón.
D. Một hình trụ.
Câu 4. Giải phương trình log2(2 + x) = 2
A. x = 6
B. x = -2
C. x = 4
D. x = 2
Câu 5. Tìm giá trị cực tiểu yCT của hàm số y = -x4 + 2x2 + 2
A. yCT = 2
B. yCT = 1
C. yCT = -2
D. yCT = -1
Câu 6. Cho tấm tôn hình chữ nhật quay quanh trục là đường thẳng chứa một cạnh của tấm tôn một góc 360° ta được một vật tròn xoay nào dưới đây?
A. Mặt trụ.
B. Hình trụ.
C. Khối trụ.
D. Khối lăng trụ.
Câu 7. Tìm tập xác định D của hàm số ![]()
A. D = (-1;+∞)
B. D = (-∞;-1)
C. D = (-∞;1)
D. D = R{-1}
Câu 8. Phương trình 2(2×2 – 3x + 1) = 1 có bao nhiêu nghiệm?
A. 0
B. 2
C. 3
D. 1
Câu 9. Tính đạo hàm của hàm số y = 5(3x + 1)

Câu 10. Tính giá trị nhỏ nhất M của hàm số y = -x3 + 3x2 + 2 trên đoạn [1;3]
A. M = 6
B. M = 2
C. M = 4
D. M = -6
Câu 11. Đường cong trong hình bên là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn phương án A, B, C, D dưới đây. Hỏi hàm số đó là hàm số nào?


Câu 12. Cho đường tròn quay quanh một đường thẳng đi qua tâm đường tròn đó một góc 360° ta được hình gì?
A. Một mặt cầu.
B. Một khối cầu.
C. Hai mặt cầu.
D. Hai khối cầu.
Câu 13. Biết đường thẳng y = x – 1 cắt đồ thị hàm số ![]() tại hai điểm phân biệt A, B có hoành độ lần lượt là xA, xB, xA < xB. Hãy tính tổng 2xA + 3xB
tại hai điểm phân biệt A, B có hoành độ lần lượt là xA, xB, xA < xB. Hãy tính tổng 2xA + 3xB
A. 2xA + 3xB = 10
B. 2xA + 3xB = 15
C. 2xA + 3xB = 1
D. 2xA + 3xB = 3
Câu 14. Tìm tiệm cận đứng và tiệm cận ngang của đồ thị hàm số ![]()
A. x = 1; y = 2
B. y = 1; x = 2
C. x = -1; y = 2
D. x = 1; y = -2
Câu 15. Hình đa diện bên có bao nhiêu mặt?

A. 6
B. 10
C. 11
D. 12
Câu 16. Tìm giá trị lớn nhất M và nhỏ nhất m của hàm số y = sin2x – cos22x + 1

Câu 17. Đường cong trong hình bên là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn phương án A, B, C, D dưới đây. Hỏi hàm số đó là hàm số nào?


Câu 18. Cho hàm số y = f(x) xác định trên R{±1}, liên tục trên mỗi khoảng xác định và có bảng biến thiên hình bên. Tìm tập hợp tất cả các giá trị thực của tham số m sao cho phương trình f(x) = m + 1 vô nghiệm.

A. [-3;0)
B. (1;+∞)
C. (-∞;-3)
D. (-2;+∞)
Câu 19. Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại A, biết SA⊥(ABC), SA = a, AB = 2a, AC = 3a. Tính bán kính r của mặt cầu ngoại tiếp hình chóp S.ABC.

Câu 20. Tính diện tích xung quanh Sxq của hình trụ có đường cao h = 2a và thể tích V = 8πa3
A. Sxq = 48πa2
B. Sxq = 36πa2
C. Sxq = 8πa2
D. Sxq = 16πa2
Câu 21. Phương trình 92x+3 = 274+x tương đương với phương trình nào sau đây?
A. 7x + 6 = 0
B. 7x – 6 = 0
C. x – 6 = 0
D. x + 6 = 0
Câu 22. Tìm tất cả các giá trị của tham số m sao cho hàm số  có tập xác định là R.
có tập xác định là R.
A. (1;+∞)
B. (-∞;1)
C. [-∞;1┤
D. [1;+∞)
Câu 23. Số tuổi của An và Bình là các nghiệm của phương trình  . Tính tổng số tuổi của An và Bình.
. Tính tổng số tuổi của An và Bình.
A. 36
B. 21
C. 12
D. 23
Câu 24. Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng 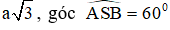

Câu 25. Tính thể tích khối chóp S.MNP biết 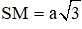

Câu 26. Cho hàm số ![]() . Khẳng định nào sau đây sai?
. Khẳng định nào sau đây sai?
A. Hàm số không có cực trị.
B. Hàm số đồng biến trên các khoảng (-∞;-1) và (-1;+∞)
C. Đồ thị hàm số có tiệm cận đứng là đường thẳng x = -1; tiệm cận ngang là đường thẳng y = 4
D. Đồ thị hàm số cắt trục hoành tại điểm ![]() và cắt trục tung tại điểm (0;-4)
và cắt trục tung tại điểm (0;-4)
Câu 27. Cho khối lăng trụ ABC.A’B’C’. Gọi M là trung điểm của AA’. Mặt phẳng (BCM) chia khối lăng trụ ABC.A’B’C’ thành hai khối. Tính tỉ số thể tích (số lớn chia số bé) của hai khối đó.
A. 6
B. 3
C. 4
D. 5
Câu 28. Cho hàm số y = f(x) có đạo hàm f'(x) = x2(x – 1)3(x + 1). Hỏi hàm số có bao nhiêu điểm cực trị?
A. 1
B. 4
C. 3
D. 2
Câu 29. Cho a, b là hai số dương khác 1. Đặt logab = m. Tính theo m giá trị của biểu thức ![]()

Câu 30. Tìm số đường tiệm cận của đồ thị hàm số ![]()
A. 1
B. 4
C. 2
D. 3
Câu 31. Cho khối lăng trụ đứng ABC.A’B’C’ có thể tích bằng a3. Biết tam giác ABC vuông tại A, AB = a, AC = 2a. Tính độ dài đường cao của khối lăng trụ.
A. 3a
B. 2a
C.
D. a
Câu 32. Cho a, b, x, y là các số thực dương khác 1. Khẳng định nào sau đây đúng?

Câu 33. Cho hàm số y = f(x) liên tục trên R và có đồ thị hàm số đường cong trong hình vẽ bên. Tìm tất cả các giá trị thực của tham số m để phương trình |f(x)| = m có 4 nghiệm phân biệt.

A. m ∈ (0;3)
B. -3 < m < 1
C. Không có giá trị nào của m.
D. 1 < m < 3
Câu 34. Cho hàm số y = ax3 + bx2 + cx + d có đồ thị như hình vẽ

A. a, b , d < 0; c > 0
B. a, b , c < 0; d > 0
C. a, c , d < 0; b > 0
D. a, d > 0; b, c < 0
Câu 35. Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số ![]() có tiệm cận đi qua điểm A(1;4)
có tiệm cận đi qua điểm A(1;4)
A. m = 4
B. m = 1
C. m = 2
D. m = 3
Câu 36. Cho hàm số y = x3 + 3x2 + mx + m – 2. Với giá trị nào của m thì hàm số có 2 điểm cực trị nằm về 2 phía trục tung.
A. m < 0
B. m > 0
C. m = 1
D. m = 0
Câu 37. Tìm tập nghiệm của bất phương trình ![]()

Câu 38. Tìm số nghiệm dương của phương trình
A. 3
B. 1
C. 2
D. 0
Câu 39. Tìm tất cả các giá trị thực của tham số m để phương trình 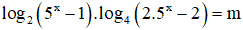
A. m ∈ (-∞;2)
B. m ∈ (2;+∞)
C. m ∈ (3;+∞)
D. m ∈ (-∞;3)
Câu 40. Tính tích các nghiệm của phương trình ![]()
![]()
Câu 41. Số lượng của một số loài vi khuẩn sau t (giờ) được tính xấp xỉ bởi đẳng thức Q = Q0.e0,195t, trong đó Q0 là số lượng vi khuẩn ban đầu. Nếu số lượng vi khuẩn ban đầu là 5000 con thì sau bao lâu có 100 000 con.
A. 24 giờ.
B. 20 giờ.
C. 3,55 giờ.
D. 15,36 giờ.
Câu 42. Cho các số thực a, b, x > 0 và b, x ≠ 1 thỏa mãn ![]() . Tính giá trị của biểu thức
. Tính giá trị của biểu thức 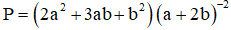

Câu 43. Cho hình lăng trụ đều ABC.A’B’C’ có ![]() . Tính thể tích khối lăng trụ ABC.A’B’C’.
. Tính thể tích khối lăng trụ ABC.A’B’C’.

Câu 44. Cho một hình lăng trụ đứng có đáy là tam giác đều. Thể tích của hình lăng trụ là V. Để diện tích toàn phần của hình lăng trụ nhỏ nhất thì cạnh đáy của lăng trụ là bao nhiêu?

Câu 45. Hàm số 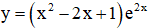
A. (0;1)
B. (0;+∞)
C. (-∞;0)
D. (-∞;+∞)
Câu 46. Cho hàm số y = lnx có đồ thị như hình 1. Đồ thị hình 2 là của hàm số nào dưới đây ?

A. y = ln|x + 1|
B. y = |ln(x + 1)|
C. y = ln|x|
D. y = |lnx|
Câu 47. Cho mặt cầu tâm O, bán kính R = a. Một hình nón có đỉnh là ở trên mặt cầu và đáy là đường tròn giao của mặt cầu đó với mặt phẳng vuông góc với đường thẳng SO tại H sao cho ![]() . Độ dài đường sinh l của hình nón bằng:
. Độ dài đường sinh l của hình nón bằng:

Câu 48. Người ta đặt được vào một hình nón hai khối cầu có bán kính lần lượt là a và 2a sao cho các khối cầu đều tiếp xúc với mặt xung quanh của hình nón, hai khối cầu tiếp xúc với nhau và khối cầu lớn tiếp xúc với đáy của hình nón. Tính bán kính đáy r của hình nón đã cho.

Câu 49. Cho hình chóp đều S.ABCD có cạnh đáy bằng a, góc giữa mặt bên với đáy bằng 45°. Gọi M, N, P lần lượt là trung điểm của SA, SB, SC. Tính thể tích của khối tứ diện AMNP.

Câu 50. Cắt một khối trụ bởi một mặt phẳng qua trục của nó, ta được thiết diện là một hình vuông có cạnh bằng 3a. Tính diện tích toàn phần của khối trụ.

Đáp án & Hướng dẫn giải:

Câu 1. Đáp án C
Phương pháp:
Xác định khoảng mà tại đó y’ ≤ 0, dấu “=” xảy ra ở hữu hạn điểm.
Cách giải:

Bảng xét dấu y’:

Hàm số nghịch biến trên khoảng (-2;0)
Câu 2. Đáp án C
Phương pháp:
Dựa vào khái niệm tâm đối xứng của khối đa diện.
Cách giải:
Hình tứ diện đều không có tâm đối xứng.
Câu 3. Đáp án B
Phương pháp:
Dựa vào khái niệm khối nón.
Cách giải:
Khi tam giác ABC quay quanh trục là đường thẳng AI một góc 360° thì các cạnh của tam giác ABC sinh ra một hình nón.
Câu 4. Đáp án D
Phương pháp:
Cách giải:
Câu 5. Đáp án A
Phương pháp:
+) Tính y’ và giải phương trình y’ = 0
+) Lập bảng xét dấu của y’ và rút ra kết luận.
+) Điểm x = x0 được gọi là điểm cực tiểu của hàm số khi và chỉ khi qua điểm đó y’ đổi dấu từ âm sang dương.
Cách giải:

Bảng xét dấu y’:

Hàm số đạt cực tiểu tại x = 0, giá trị cực tiểu yCT = y(0) = 2
Câu 6. Đáp án C
Phương pháp:
Dựa vào khái niệm khối trụ.
Cách giải:
Cho tấm tôn hình chữ nhật quay quanh trục là đường thẳng chứa một cạnh của tấm tôn một góc 360° ta được một khối trụ.
Câu 7. Đáp án A
Phương pháp:
Tập xác định của hàm số y = xα:
+) Nếu α là số nguyên dương thì TXĐ: D = R
+) Nếu α là số nguyên âm hoặc bằng 0 thì TXĐ: D = R{0}
+) Nếu α là số không nguyên thì TXĐ: D = (0;+∞)
Cách giải:
![]() : Điều kiện xác định: x + 1 > 0 ⇔ x > -1
: Điều kiện xác định: x + 1 > 0 ⇔ x > -1
TXĐ: D = (-1;+∞)
Câu 8. Đáp án B
Phương pháp: ax = b ⇔ x = logab (0 < a ≠ 1; b > 0)
Cách giải:

Vậy, phương trình đã cho có 2 nghiệm.
Câu 9. Đáp án D
Phương pháp:
Cách giải:
Câu 10. Đáp án B
Phương pháp:
– Tìm TXĐ
– Tìm nghiệm và các điểm không xác định của y’.
– Tính giá trị của hàm số tại các điểm trên, từ đó đánh giá giá trị nhỏ nhất của hàm số trên đoạn [1;3]
Cách giải:

Câu 11. Đáp án A
Phương pháp:
Nhận biết dạng của hàm số bậc ba và hàm số bậc 4 trùng phương.
Cách giải:
Quan sát đồ thị hàm số, ta thấy: đồ thị hàm số không phải đồ thị của hàm số bậc 4 trùng phương ⇒ Loại phương án C
Khi x → +∞ thì y → +∞ nên a > 0 ⇒ Loại phương án B
Đồ thị hàm số có 2 điểm cực trị, trong đó 1 cực trị tại x = 0, 1 cực trị tại x = x0 > 0
Xét  Loại phương án D
Loại phương án D
Câu 12. Đáp án A
Phương pháp:
Dựa vào khái niệm khối cầu.
Cách giải:
Cho đường tròn quay quanh một đường thẳng đi qua tâm đường tròn đó một góc 360° ta được hình là một mặt cầu.
Câu 13. Đáp án B
Phương pháp:
Giải phương trình hoành độ giao điểm, từ đó tính tổng 2xA + 3xB
Cách giải:
Xét phương trình hoành độ giao điểm của đường thẳng y = x – 1 và đồ thị hàm số ![]()

Câu 14. Đáp án C
Phương pháp:
Hàm số bậc nhất trên bậc nhất ![]() có 1 TCĐ là
có 1 TCĐ là ![]() và 1 TCN là
và 1 TCN là ![]()
Cách giải:
Đồ thị hàm số ![]() có tiệm cận đứng và tiệm cận ngang lần lượt là x = -1; y = 2
có tiệm cận đứng và tiệm cận ngang lần lượt là x = -1; y = 2
Câu 15. Đáp án C
Phương pháp:
Đếm các mặt của đa diện.
Cách giải:
Hình đa diện bên có 11 mặt.
Câu 16. Đáp án C
Phương pháp:
Đặt sin2x = t, t ∈ [-1;1], khảo sát, tìm giá trị nhỏ nhất, lớn nhất của hàm số với ẩn là t.
Cách giải: y = sin2x – cos22x + 1 = sin22x + sin2x
Đặt sin2x = t, t ∈ [-1;1], ta có: ![]()
Ta có:

Câu 17. Đáp án A
Phương pháp:
Loại trừ từng đáp án.
Cách giải:
+) Đồ thị hàm số y = x4 có dạng là hình parabol ⇒ Loại phương án B
+) 
+) Đồ thị hàm số y = 2x luôn đồng biến trên R ⇒ Loại phương án D
Câu 18. Đáp án A
Phương pháp:
Số nghiệm của phương trình f(x) = m + 1 bằng số giao điểm của đồ thị hàm số y = f(x) và đường thẳng y = m + 1
Cách giải:
Phương trình f(x) = m + 1 vô nghiệm ⇔ -2 ≤ m + 1 < 1 ⇔ -3 ≤ m < 0
Câu 19. Đáp án D

Phương pháp:
S.ABC là tứ diện vuông là một phần của hình hộp chữ nhật SB’D’C’.ABDC (như hình vẽ bên), có tâm mặt cầu ngoại tiếp trùng với tâm của hình hộp chữ nhật, có bán kính bằng nửa đường chéo của hình hộp chữ nhật (độ dài các cạnh là a, b, c) bằng 
Cách giải:
Bán kính r của mặt cầu ngoại tiếp hình chóp S.ABC:

Câu 20. Đáp án C
Phương pháp:
Diện tích xung quanh Sxq của hình trụ: Sxq = 2πrh
Thể tích của hình trụ: V = πr2 h
Cách giải:
Hình trụ có V = 8πa3 ⇔ πr2h = 8πa3 ⇔ πr2.2a = 8πa3 ⇔ r2 = 4a2 ⇔ r = 2a
Diện tích xung quanh Sxq của hình trụ: Sxq = 2πrh = 2π.2a.2a = 8πa2
Câu 21. Đáp án C
Phương pháp:
Hai phương trình tương đương là hai phương trình có cùng tập nghiệm.
Cách giải:

Câu 22. Đáp án A
Phương pháp:

Cách giải:
Điều kiện xác định:

Để hàm số có tập xác định là R thì

Câu 23. Đáp án A
Phương pháp:
+) Tìm TXĐ.
+) Đặt log3x = t, quy đồng, giải phương trình ẩn t, từ đó suy ra nghiệm x.
Cách giải:
ĐKXĐ: 
Đặt log3x = t (t ≠ 5, t ≠ -1). Khi đó, phương trình  trở thành:
trở thành:

Tổng số tuổi của An và Bình là: 9 + 27 = 36 (tuổi)
Câu 24. Đáp án B
Phương pháp: ![]()
Cách giải:

S.ABCD là chóp tứ giác đều ⇒ ABCD là hình vuông

Thể tích của khối nón đỉnh S có đáy là đường tròn ngoại tiếp tứ giác ABCD:

Câu 25. Đáp án B
Phương pháp:
+) Gọi I là trung điểm của MN ⇒ SI ⊥ (MNP)
+) Tính diện tích tam giác MNP.
+) ![]()
Cách giải:

ΔSMN vuông cân tại S và nằm trong mặt phẳng vuông góc với mặt phẳng đáy, gọi I là trung điểm của MN ⇒ SI⊥(ABC) và 

Câu 26. Đáp án C
Phương pháp:
Dựa vào các đường tiệm cận của đồ thị hàm số và tính đơn điệu của đồ thị hàm số.
Cách giải:
Đồ thị hàm số có tiệm cận đứng là đường thẳng x = -1 và tiệm cận ngang là đường thẳng y = 4 là khẳng định sai. (do đồ thị hàm số có tiệm cận đứng là đường thẳng x = -1 và tiệm cận ngang là đường thẳng y = 3).
Câu 27. Đáp án D
Phương pháp:
Lập tỉ lệ thể tích của hai khối trên với thể tích của khối lăng trụ ABC.A’B’C’ .
Cách giải:


Câu 28. Đáp án D
Phương pháp:
Xác định số điểm mà tại đó f'(x) đổi dấu
Cách giải:
 đổi dấu tại 2 điểm x = 1, x = -1. Do đó, hàm số có 2 điểm cực trị.
đổi dấu tại 2 điểm x = 1, x = -1. Do đó, hàm số có 2 điểm cực trị.
Câu 29. Đáp án B
Phương pháp:
![]()
Cách giải:

Câu 30. Đáp án C
Phương pháp:
* Định nghĩa tiệm cận ngang của đồ thị hàm số y = f(x)
Nếu ![]() là TCN của đồ thị hàm số.
là TCN của đồ thị hàm số.
* Định nghĩa tiệm cận đứng của đồ thị hàm số y = f(x)
Nếu ![]() thì x = a là TCĐ của đồ thị hàm số.
thì x = a là TCĐ của đồ thị hàm số.
Cách giải:
TXĐ: D = R

Đồ thị hàm số  có 2 đường tiệm cận là
có 2 đường tiệm cận là ![]()
Câu 31. Đáp án D
Phương pháp:
Thể tích khối lăng trụ: V = Sđáy.h
Cách giải:

Câu 32. Đáp án A
Phương pháp:
Dựa vào các công thức liên quan đến logarit.
Cách giải:
Khẳng định đúng là: ![]() , với a, b, x, y là các số thực dương khác 1.
, với a, b, x, y là các số thực dương khác 1.
Câu 33. Đáp án D
Phương pháp:
Số nghiệm của phương trình |f(x)| = m bằng số giao điểm của đồ thị hàm số y = |f(x)| và đường thẳng y = m
Cách giải:

Từ đồ thị hàm số y = f(x) ta có đồ thị hàm số y = |f(x)| như hình bên:
Số nghiệm của phương trình |f(x)| = m bằng số giao điểm của đồ thị hàm số y = |f(x)| và đường thẳng y = m
⇒ Để phương trình |f(x)| = m có 4 nghiệm phân biệt thì 1 < m < 3
Câu 34. Đáp án D
Phương pháp:
Nhận dạng hàm số bậc ba.
Cách giải:
Quan sát đồ thị hàm số, ta thấy: khi x → +∞ thì y → +∞ nên a > 0 ⇒ Loại các đáp án A, B, C. Chọn D.
Câu 35. Đáp án B
Phương pháp:
Xác định các trường hợp của m, trong mỗi trường hợp, tìm các đường tiệm cận của đồ thị hàm số và cho các đường tiệm cận đi qua điểm A(1;4)
Cách giải:
+) Với m = 0 ⇒ y = 4: Đồ thị hàm số không có tiệm cận.
+) Với m = 4 thì y = 4: Đồ thị hàm số không có tiệm cận.
+) Với ![]() có tiệm cận đứng
có tiệm cận đứng ![]() , tiệm cận ngang y = m
, tiệm cận ngang y = m
Giả sử TCĐ ![]() đi qua
đi qua ![]()
Giả sử TCN y = m đi qua A(1;4) ⇒ m = 4 (loại)
Kết luận: m = 1
Câu 36. Đáp án A
Phương pháp:
Hàm số bậc ba có 2 điểm cực trị nằm về 2 phía trục tung khi và chỉ khi phương trình y’ = 0 có hai nghiệm trái dấu.
Cách giải:
y = x3 + 3x2 + mx + m – 2 ⇒ y’ = 3x2 + 6x + m
Hàm số bậc ba có 2 điểm cực trị nằm về 2 phía trục tung khi và chỉ khi phương trình y’ = 0 có hai nghiệm trái dấu ⇔ ac < 0
⇔ 3.m < 0 ⇔ m < 0
Câu 37. Đáp án D
Phương pháp:
+) Tìm TXĐ.
+) Đưa phương trình về ẩn log5x
Cách giải:
ĐKXĐ: x > 0, x ≠ 1

Câu 38. Đáp án B
Phương pháp:
Nhóm nhân tử chung, đưa về phương trình mũ cơ bản để giải.
Cách giải:

Số nghiệm dương của phương trình đã cho là 1.
Câu 39. Đáp án C
Phương pháp:
Biến đổi, đặt
Cách giải:

f'(t) = 2t + 1 > 0, ∀ t ≥ 2 ⇒ Hàm số đồng biến trên khoảng [2;+∞)

Để phương trình (*) có nghiệm thì 2m ≥ 6 ⇔ m ≥ 3
Câu 40. Đáp án A
Phương pháp: ![]()
Cách giải:

Câu 41. Đáp án D
Phương pháp:
Giải phương trình mũ cơ bản.
Cách giải:

Câu 42. Đáp án D
Phương pháp:

Cách giải:


Câu 43. Đáp án B
Phương pháp: VABC.A’B’C’ = AA’.SABC
Cách giải:
ABC.A’B’C’ là lăng trụ đều ⇒ ΔABC đều 
Thể tích ABC.A’B’C’: ![]()
Câu 44. Đáp án C
Phương pháp:
Thể tích hình lăng trụ V = Sh
Diện tích toàn phần của lăng trụ: Stp = Sxq + 2.Sđáy
Cách giải:
Giả sử hình lăng trụ có đáy là tam giác đều cạnh a, có chiều cao h.

(áp dụng bất đẳng thức Cô- si cho 3 số dương)
Dấu “=” xảy ra khi và chỉ khi 
Câu 45. Đáp án A
Phương pháp:
Phương pháp xét sự đồng biến, nghịch biến của các hàm số:
– Bước 1: Tìm tập xác định, tính f'(x)
– Bước 2: Tìm các điểm tại đó f'(x) = 0 hoặc f'(x) không xác định
– Bước 3: Sắp xếp các điểm đó theo thứ tự tăng dần và lập bảng biến thiên
– Bước 4: Kết luận về các khoảng đồng biến, nghịch biến của hàm số.
Cách giải:

Bảng xét dấu y’:

Hàm số y = (x2 – 2x + 1)e2x nghịch biến trên khoảng (0;1)
Câu 46. Đáp án D
Phương pháp:
Dựa vào cách vẽ đồ thị hàm số các hàm có chứa trị tuyệt đối.
Cách giải:
Đồ thị hình 2 là của hàm số y = |lnx| được dựng từ đồ thị ở Hình 1, bằng cách: giữ nguyên phần đồ thị nằm phía trên trục hoành, lấy đối xứng phần đồ thị nằm phía dưới trục hoành qua trục hoành.
Câu 47. Đáp án B
Phương pháp: ![]()
Cách giải:


Câu 48. Đáp án B
Cách giải:

Ta có: O1E ⊥ SB, O2E ⊥ SB ⇒ O1E//O2E
Mà ![]() là đường trung bình của tam giác SO2F
là đường trung bình của tam giác SO2F
⇒ SO1 = O1O2 = a + 2a = 3a

Câu 49. Đáp án A
Phương pháp:
– Lập tỉ lệ thể tích khối tứ diện AMNP với khối chóp S.ABCD
– Tính thể tích khối chóp S.ABCD
– Tính thể tích khối tứ diện AMNP.
Cách giải:


Ta có: 

Câu 50. Đáp án B
Phương pháp:
Diện tích xung quanh của khối trụ Sxq = 2πrh
Diện tích toàn phần của khối trụ: Stp = Sxq + S2đáy
Cách giải:

Khối trụ có đường cao h = 3a, bán kính đáy ![]()

Trên đây là một số Đề thi học kì 1 môn Toán lớp 12 năm học 2022-2023. Các em học sinh có thể tham khảo trong quá trình học tập.
Đăng bởi: Thcs-thptlongphu.edu.vn
Chuyên mục: Tổng hợp