Giải bài tập trang 147, 148 bài 6 tam giác cân Sách Bài Tập Toán lớp 7 tập 1. Câu 75: Cho tam giác ABC cân tạiA) Vẽ điểm D sao cho A là trung điểm của BD. Tính số đo góc BCD…
Câu 75 trang 147 Sách Bài Tập (SBT) Toán lớp 7 tập 1
Cho tam giác ABC cân tạiA) Vẽ điểm D sao cho A là trung điểm của BD. Tính số đo góc BCD
Giải
Bạn đang xem: Giải bài 75, 76, 77, 78 trang 147, 148 SBT Toán lớp 7 tập 1
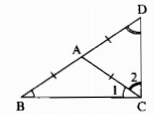
Ta có: ∆ABC cân tại A
( Rightarrow widehat B = widehat {{C_1}}) (tính chất tam giác cân)
Lại có: AD = AB (gt)
=>AD = AC do đó ∆ACD cân tại A
( Rightarrow widehat D = widehat {{C_2}}) (tính chất tam giác cân)
Mà (widehat {BC{rm{D}}} = widehat {{C_1}} + widehat {{C_2}})
Nên (widehat {BC{rm{D}}} = widehat B + widehat D) (1)
Trong ∆BCD, ta có:
(widehat B + widehat D + widehat {BC{rm{D}}} = 180^circ ) (tổng ba góc trong tam giác) (2)
Từ (1) và (2) suy ra: (2widehat {BC{rm{D}}} = 180^circ ) hay (widehat {BC{rm{D}}} = 90^circ )
Câu 76 trang 147 Sách Bài Tập (SBT) Toán lớp 7 tập 1
Cho tam giác ABC cân tại A có cạnh bên bằng 3cm. Gọi D là một điểm thuộc đáy BC. Qua D, kẻ các đường thẳng song song với các cạnh bên, chúng cắt AB và AC theo thứ tự tại F và E. Tính tổng DE + DF.
Giải

Ta có: DF // AC (gt)
( Rightarrow widehat {{D_1}} = widehat C) (hai góc đồng vị) (1)
Lại có: ∆ABC cân tại A
( Rightarrow widehat B = widehat C) (tính chất tam giác cân) (2)
Từ (1) và (2) suy ra: (widehat B = widehat {{D_1}})
Hay ∆BFD cân tại F => BF = DF
Nối AD. Xét ∆AFD và ∆DEA, ta có:
(widehat {A{rm{D}}F} = widehat {E{rm{AD}}}) (so le trong vì DF // AC)
AD cạnh chung
(widehat {F{rm{D}}A} = widehat {E{rm{D}}A}) (so le trong vì DE // AB)
Suy ra: ∆ADF = ∆DAE (g.c.g) => AF = DF (hai cạnh tương ứng)
Vậy: DE + DF = AF + BF = AB = 3(cm)
Câu 77 trang 148 Sách Bài Tập (SBT) Toán lớp 7 tập 1
Cho tam giác đều ABC. Lấy các điểm D, E, F theo thứ tự thuộc các cạnh AB, BC, CA sao cho AD = BE = CF. Chứng minh rằng ∆DEF là tam giác đều.
Giải

Ta có: AB = AD + DB (1)
BC = BE + EC (2)
AC = AF + FC (3)
AB = AC = BC (gt) (4)
AD = BE = CF (gt) (5)
Từ (1), (2), (3), (4) và (5) suy ra:
BD = EC = AF
Xét ∆ADF và ∆BED, ta có:
AD = BE (gt)
(widehat A = widehat B = 60^circ ) (vì ∆ABC đều)
AE = BD (chứng minh trên)
Suy ra: ∆ADF = ∆BED (c.g.c)
Suy ra: DF = DE (hai cạnh tương ứng) (6)
Xét ∆ADF và ∆CFE ta có:
AD = CF (gt)
(widehat A = widehat C = 60^circ ) (vì ∆ABC đều)
EC = AF (chứng minh trên)
Suy ra : ∆ADF = ∆CFE (c.g.c)
Suy ra: DF = FE (hai cạnh tương ứng) (7)
Từ (6) và (7) suy ra: DF = ED = FE
Vậy ∆DEF đều.
Câu 78 trang 148 Sách Bài Tập (SBT) Toán lớp 7 tập 1
Cho tam giác ABC. Các tia phân giác của các góc B và C cắt nhau ở I. Qua I kẻ đường thẳng song song với BC. Gọi giao điểm của đường thẳng này với AB, AC theo thứ tự là D, E. Chứng minh rằng DE = BD + CE
Giải

Ta có: DI // BC (gt)
( Rightarrow widehat {{I_1}} = widehat {{B_1}}) (so le trong) (1)
Lại có: ({widehat B_1} = widehat {{B_2}}) (2)
(vì BI là tia phân giác của (widehat B))
Từ (1) và (2) suy ra: (widehat {{I_1}} = widehat {{B_2}})
( Rightarrow ) ∆BDI cân tại D => BD = DI (3)
Mà IE // BC (gt) => (widehat {{I_2}} = widehat {{C_1}}) (so le trong) (4)
Đồng thời: (widehat {{C_1}} = widehat {{C_2}}) (Vì CI là tia phân giác của (widehat {{C_1}})) (5)
Từ (4) và (5) suy ra: (widehat {{I_2}} = widehat {{C_2}}) => ∆CEI cân tại E
( Rightarrow ) CE = EI (hai cạnh tương ứng) (6)
Từ (3) và (6) suy ra: BD + CE = DI + EI = DE.
Trường
Đăng bởi: Thcs-thptlongphu.edu.vn
Chuyên mục: Tổng hợp





