Giải bài tập trang 66, 67 bài 4 Tính chất ba đường trung tuyến của tam giác Sách giáo khoa (SGK) Toán 7. Câu 23: Cho G là trọng tâm của tam giác DEF với đường trung tuyến DH…
Bài 23 trang 66 sgk toán lớp 7- tập 2
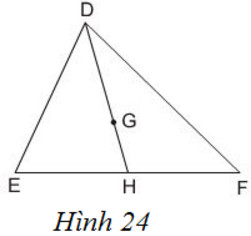
23. Cho G là trọng tâm của tam giác DEF với đường trung tuyến DH. Trong các khẳng định sau đây, khẳng định nào đúng ?
(frac{DG}{DH}= frac{1}{2}); (frac{DG}{GH}) = 3
Bạn đang xem: Giải bài 23, 24, 25, 26, 27 trang 66, 67 SGK Toán 7
(frac{GH}{DH}= frac{1}{3}); (frac{GH}{DG}= frac{2}{3})
Hướng dẫn:
G là trọng tâm của tam giác DEF với đường trung tuyến DH. Ta có:
(frac{GD}{DH}= frac{2}{3}) vì (frac{GH}{DH}= frac{1}{3})
Vậy khẳng định (frac{GH}{DH}= frac{1}{3}) là đúng
Các khẳng định còn lại sai
Bài 24 trang 66 sgk toán lớp 7- tập 2
24. Cho hình bên. Hãy điền số thích hợp vào chỗ trống trong các đẳng thức sau:
a) MG = … MR ; GR = …MR ; GR = …MG
b) NS = ..NG; NS = …GS; NG = GS

Hướng dẫn
Hình vẽ cho ta biết hai đường trung tuyến MR và NS cắt nhau tại G nên G là trọng tâm của tam giác. Vì vậy ta điền số như sau:
a) MG =(frac{2}{3}) MR ; GR = (frac{1}{3}) MR ; GR =(frac{1}{2}) MG
b) NS =(frac{2}{3}) NG; NS =3GS; NG =2GS
Bài 25 trang 67 sgk toán lớp 7- tập 2
25. Biết rằng: Trong một tam giác vuông, đường trung tuyến ứng với cạnh bằng một nửa cạnh huyền. hãy giải bài toán sau:
Cho tam giác vuông ABC có hai cạnh góc vuông AB = 3cm, AC = 4cm. Tính cách từ đỉnh A tới trọng tâm G của tam giác ABC.
Hướng dẫn:
∆ABC vuông tại A => BC2 = AB2 + AC2
BC2 = 32 + 42
BC2 = 25
BC = 5

Gọi M là trung điểm của BC => AM là trung tuyến ứng với cạnh huyền bằng một nửa cạnh huyền nên AM = (frac{1}{2}) BC
Vì G là trọng tâm của ∆ ABC nên AG =(frac{2}{3}) AM => AG =(frac{2}{3}).(frac{1}{2}) BC
=> AG = (frac{1}{3}) BC = (frac{1}{3}) .5 = 1.7cm
Bài 26 trang 67 sgk toán lớp 7- tập 2
26. Chứng minh định lí: Trong một tam giác cân, hai đường trung tuyến ứng với hai cạnh bên thì bằng nhau.
Hướng dẫn:
Giả sử ∆ABC cân tại A có hai đường trung tuyến BM và CN, ta chứng minh BM = CN

Vì ∆ ABC cân tại A=> AB = AC mà M, N là trung điểm AC, AB nên CM = BN
Do đó ∆CMB ;∆BNC có:
BC chung
CM = BN (cm trên)
AB = AC (∆ABC cân)
=> BM = CN
Bài 27 trang 67 sgk toán lớp 7- tập 2
27. Hãy chứng minh định lí đảo của định lí trên : Nếu tam giác có hai đường trung tuyến bằng nhau thì tam giác đó cân.
Hướng dẫn:
Giả sử ∆ABC có hai đường trung tuyến BM và CN gặp nhau ở G
=> G là trọng tâm của tam giác
=> GB = BM; GC = CN
mà BM = CN (giả thiết) nên GB = GC
=> ∆GBC cân tại G => (widehat{GCB} = widehat{GBC})
do đó ∆BCN = ∆CBM vì:
BC là cạnh chung
CN = BM (gt)
(widehat{GCB} = widehat{GBC}) (cmt)
=> (widehat{NBC} = widehat{MCB}) => ∆ABC cân tại A
Trường
Đăng bởi: Thcs-thptlongphu.edu.vn
Chuyên mục: Tổng hợp





