Giải bài tập trang 158 bài 1 Sự xác định đường tròn. Tính chất đối xứng của đường tròn Sách bài tập (SBT) Toán 9 tập 2. Câu 13: Tam giác ABC cân tại A, BC = 12cm, đường cao AH = 4cm. Tính bán kính của đường tròn ngoại tiếp tam giác ABC…
Câu13* trang 158 Sách bài tập (SBT) Toán 9 Tập 1
Tam giác ABC cân tại A, BC = 12cm, đường cao AH = 4cm. Tính bán kính của đường tròn ngoại tiếp tam giác ABC.
Giải:
Bạn đang xem: Giải bài 13, 14, 1.1 trang 158 SBT Toán 9 tập 2
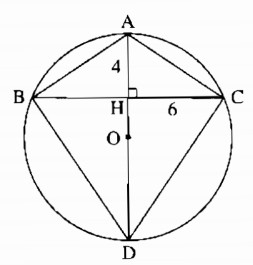
Kéo dài đường cao AH cắt đường tròn ngoại tiếp tam giác ABC tại D. Goi O là tâm đường tròn ngoại tiếp tam giác ABC.
Vì tam giác ABC cân tại A nên AH là đường trung trực của BC. Suy ra AD là đường trung trực của BC.
Khi đó O thuộc AD hay AD là đường kính của đường tròn ngoại tiếp tam giác ABC.
Tam giác ACD nội tiếp trong (O) có AD là đường kính suy ra: (widehat {ACD} = 90^circ )
Tam giác ACD vuông tại C nên theo hệ thức liên hệ giữa đường cao và hình chiếu, ta có:(C{H^2} = HA.HD)
Suy ra:(HD = {{C{H^2}} over {HA}} = {{{{left( {{{BC} over 2}} right)}^2}} over {HA}})
=({{{{left( {{{12} over 2}} right)}^2}} over 4} = {{{6^2}} over 4} = {{36} over 4} = 9) (cm)
Ta có: AD = AH +HD = 4 + 9 = 13 (cm)
Vậy bán kính của đường tròn (O) là: (R = {{AD} over 2} = {{13} over 2} = 6,5) (cm)
Câu 14* trang 158 Sách bài tập (SBT) Toán 9 Tập 1
Cho đường tròn (O) và hai điểm A, B nằm bên ngoài đường tròn. Dựng đường kính COD sao cho AC = BD.
Giải:

* Cách dựng
− Dựng đối xứng với A quan tâm O của đường tròn.
− Dựng đường thẳng x là đường trung trực của A’B.
− Gọi giao điểm của đường thẳng x và đường tròn (O) là D.
− Dựng đường kính COD.
* Chứng minh
Ta có: OA = OA’ và OD = OC
Suy ra tứ giác ACA’D là hình bình hành.
Suy ra: AC = A’D
Lại có: A’D = DB (tính chất đường trung trực)
Suy ra: AC = BD.
Câu 1.1 trang 158 Sách bài tập (SBT) Toán lớp 9 Tập 1
Xét tính đúng – sai của mỗi khẳng định sau:
Cho tam giác ABC nội tiếp đường tròn (O).
a) Nếu BC là đường kính của đường tròn thì (widehat {BAC} = 90^circ ).
b) Nếu AB = AC thì AO vuông góc với BC.
c) Nếu tam giác ABC không vuông góc thì điểm O nằm bên trong tam giác đó.
Giải:
a) Đúng ; b) Đúng ; c) Sai.
Trường
Đăng bởi: Thcs-thptlongphu.edu.vn
Chuyên mục: Tổng hợp





