Giải bài 1, 2, 3, 4, 5 trang 107, 108 SGK Toán 7

Giải bài tập trang 107, 108 bài 1 Tổng ba góc của một tam giác Sách giáo khoa (SGK) Toán 7. Câu 1: Tính số đo…

Bài 1 trang 107 – Sách giáo khoa toán 7 tập 1

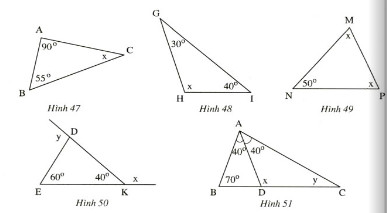
Tính số đo (x) và (y) ở các hình 47.48.49,50,51:

Bạn đang xem: Giải bài 1, 2, 3, 4, 5 trang 107, 108 SGK Toán 7

Giải:

Hình 47) 

Theo định lí tổng ba góc trong một tam giác ta được:
(x + {{90}^0} + {{55}^{0}} = {{180}^0})
(Rightarrow x = {{180}^0} – left( {{{90}^0} + {{55}^0}} right) = {{35}^0})

Hình 48) 

Theo định lí tổng ba góc trong một tam giác ta được:

(x + {rm{ }}{{40}^0} + {rm{ }}{{30}^0} = {rm{ }}{{180}^0})
(= > {rm{ }}x = {rm{ }}{{180}^0}{rm{ – }}left( {{rm{ }}{{40}^0} + {rm{ }}{{30}^0}} right) = {rm{ }}{{110}^0})

Hình 49)

Theo định lí tổng ba góc trong một tam giác ta được:

(x + {rm{ }}x + {rm{ }}{{50}^0} = 180^0)
( Rightarrow {rm{ }}2x = {rm{ }}{{180}^0} – {{50}^0} = {{130}^0}) 

(x = {65}^0)

Hình 50) 

Vì (y) là góc ngoài tam giác tại đỉnh (D) nên ta có:

(y = {rm{ }}{60^0} + {rm{ }}{40^0} = {rm{ }}{100^0})

Hai góc (x) và (widehat{DKE}) là hai góc kề bù nên:

(x + {{40}^0} ={180}^{0})

(x = {{180}^0} – {{40}^{0}} = 140^0)

Hình 51)

Áp dụng định lí tổng ba góc trong một tam giác vào (Delta  ABC) ta có:

(widehat A + widehat B + widehat C=180^0)

(({40^0} + {rm{ }}{40^0}){rm{ }} + {rm{ }}{70^0} + {rm{ }}y{rm{ }} = {180^0})

(y+  150^0 =180^0)

(y = {180^{0}} – {rm{ }}{150^0} = {rm{ }}{30^{0}})

Áp dụng định lí tổng ba góc trong một tam giác vào (Delta  ACD) ta có:

(x + {rm{ }}{40^0} + {rm{ }}{30^0} = {rm{ }}{180^0})

(x = {rm{ }}{180^0} – ({rm{ }}{40^0} + {rm{ 3}}{0^0}) = {rm{ }}{110^0})

 

---

Bài 2 trang 108 – Sách giáo khoa toán 7 tập 1

Cho tam giác (ABC): (widehat{B}= 80^0), (widehat{C}=  30^0). Tia phân giác của góc (A) cắt (BC) ở (D). Tính (widehat{ADC},widehat{ADB}).

Giải:

Theo định lí tổng ba góc trong một tam giác ta có:

(widehat {BAC} + widehat B + widehat C = {180^0})

(widehat{BAC}= 180^0- (widehat{B}+widehat{C})) = (180^0-( 80^0+ 30^0)= 70^0) 

Vì (AD) là tia phân giác của (widehat{BAC}) nên (widehat{A_{1}})=(widehat{A_{2}})

(widehat{A_{1}})=(widehat{A_{2}})=(frac{widehat{BAC}}2)=(frac{70^{0}}2= 35^0)

(widehat{ADC}) = (widehat{B}) + (widehat{A_{1}})(Góc ngoài của tam giác)

(=80^0+ 35^0= 115^0)

Hai góc (widehat{ADC}) và (widehat{ADB}) là hai góc kề bù 

Do đó (widehat{ADB}=  180^0- widehat{ADC}= 180^0-115^0=65^0)

 

                

---

Bài 3 trang 108 – Sách giáo khoa toán 7 tập 1

Cho hình 52. Hãy so sánh: 

a) (widehat{BIK}) và (widehat{BAK}).

b) (widehat{BIC}) và (widehat{BAC})

Giải

a)Ta có (widehat{BIK}) là góc ngoài của (Delta  BAI).

Nên  (widehat{BIK}=widehat{BAI }+widehat{ABI }> widehat{BAI })       (1)

(widehat{BAK}=widehat{BAI }) 

Vậy (widehat{BIK}>widehat{BAK})

b) Ta có (widehat{CIK }) là góc ngoài (Delta AIC)

nên (widehat{CIK }=widehat{CAI}+widehat{ICA}>widehat{CAI})      (2)

Từ (1) và (2) ta có:

(widehat{BIK})  + (widehat{CIK } > widehat{BAI }) + (widehat{CAI})

(Rightarrow widehat{BIC} > widehat{BAC}).

 

---

Bài 4 trang 108 – Sách giáo khoa toán 7 tập 1

Tháp nghiêng Pi – da ở Italia nghiêng (5^0)  so với  phương thẳng đứng(h.53). Tính số đo của góc (ABC) trên hình vẽ.

Giải:

Ta có tam giác vuông (ABC) vuông ở (C) nên

 (widehat{A})+ (widehat{B}=  90^0) (vì hai góc nhọn trong tam giác vuông phụ nhau)

Hay  (5^0)+(widehat{B}) =  (90^0) (Rightarrow {90^0} – {5^0} = {85^0})

 

 

---

Bài 5 trang 108 – Sách giáo khoa toán 7 tập 1

 Ta gọi tam giác có ba góc nhọn là tam giác nhọn, tam giác có một góc tù là tam giác tù. Gọi tên tam giác nhọn, tam giác tù, tam giác vuông trên hình 54.

Giải:

 a) Áp dụng định lí tổng ba góc của một tam giác vào tam giác (ABC) ta đươc:

$$eqalign{
& widehat A + widehat B + widehat C = {180^0} cr
& Rightarrow widehat A = {180^0} – widehat B – widehat C = {180^0} – {62^0} – {28^0} = {90^0} cr} $$

Do đó tam giác (ABC) vuông tại (A).

b)  Áp dụng định lí tổng ba góc của một tam giác vào tam giác (DEF) ta đươc:                

$$eqalign{
& widehat D + widehat E + widehat F = {180^0} cr
& Rightarrow widehat D = {180^0} – widehat E – widehat F = {180^0} – {45^0} – {37^0} = {98^0} cr} $$

Do đó tam giác (DEF) tù                

c) Áp dụng định lí tổng ba góc của một tam giác vào tam giác (HKI) ta đươc:      

$$eqalign{
& widehat H + widehat K + widehat I = {180^0} cr
& Rightarrow widehat H = {180^0} – widehat K – widehat I = {180^0} – {38^0} – {62^0} = {82^0} cr} $$

Do đó tam giác (HIK) nhọn.

 

Trường

Giải bài tập