Giải bài 1, 2, 3, 4, 5, 6, 7, 8, 9 trang 57, 58 SGK Toán 7 tập 2 – CTST

Giải bài tập trang 57, 58 Bài 2 Tam giác bằng nhau sgk toán 7 tập 2 chân trời sáng tạo. Bài 1 Quan sát Hình 23 rồi thay dấu ? bằng tên tam giác thích hợp.

Bài 1 trang 57 sách giáo khoa Toán 7 Chân trời sáng tạo tập 2

Quan sát Hình 23 rồi thay dấu ? bằng tên tam giác thích hợp.

a) $△$ABE = $△$?

Bạn đang xem: Giải bài 1, 2, 3, 4, 5, 6, 7, 8, 9 trang 57, 58 SGK Toán 7 tập 2 – CTST

b) $△$EAB = $△$?

c) $△$? = $△$CDE. 

Lời giải: 

Quan sát Hình 23 ta thấy:

a) Xét ∆ABE và ∆DCE có:

AB = DC (theo giả thiết).

BE = CE (theo giả thiết).

AE = DE (theo giả thiết).

Suy ra ∆ABE = ∆DCE (c.c.c).

Vậy ∆ABE = ∆DCE.

b) Do ∆ABE = ∆DCE (chứng minh trên) nên ∆EAB = ∆EDC.

c) Do ∆ABE = ∆DCE (chứng minh trên) nên ∆BAE = ∆CDE.

Bài 2 trang 57 sách giáo khoa Toán 7 Chân trời sáng tạo tập 2

Cho (Delta{DEF}=Delta{HIK}) và (widehat D= {73^o}), DE = 5cm, IK = 7cm. Tính số đo (widehat H) và độ dài HI, EF.

Lời giải: 

Vì (Delta{DEF}=Delta{HIK})

( Rightarrow widehat D = widehat H)( 2 góc tương ứng )

Mà (widehat D =73^0)

( Rightarrow widehat H=73^0)

Vì (Delta{DEF}=Delta{HIK})

 (Rightarrow DE = HI;EF = IK;DF = HK)( các cạnh tương ứng )

Vậy ( widehat H = {73^o};HI = 5cm;EF = 7cm)

Bài 3 trang 58 sách giáo khoa Toán 7 Chân trời sáng tạo tập 2

Cho hai tam giác bằng nhau ABC và DEF (các đỉnh chưa viết tương ứng), trong đó (widehat A = widehat E), (widehat C = widehat D). Tìm các cặp cạnh bằng nhau, cặp góc tương ứng bằng nhau còn lại.

Lời giải: 

Vì (widehat A = widehat E), (widehat C = widehat D) nên đỉnh A tương ứng với đỉnh E, đỉnh C tương ứng với đỉnh D. 

( Rightarrow widehat B = widehat F) ( 2 góc tương ứng)

Do đó, (Delta{ABC}=Delta{EFD})

(Rightarrow AB = DE;BC = EF;AC = DF)( các cạnh tương ứng )

Bài 4 trang 58 sách giáo khoa Toán 7 Chân trời sáng tạo tập 2

Cho biết (Delta{MNP}=Delta{DEF}) và MN = 4cm, MP = 5cm, EF = 6cm. Tính chu vi tam giác MNP.

Lời giải: 

Vì (Delta{MNP}=Delta{DEF}) 

( Rightarrow DE = MN;EF = NP;DF = MP) (các cạnh tương ứng)

( Rightarrow NP = 6cm)

( Rightarrow ) Chu vi tam giác MNP là:

C = MN + MP + NP = 4 + 5 + 6 = 15 (cm)

Bài 5 trang 58 sách giáo khoa Toán 7 Chân trời sáng tạo tập 2

Cho đoạn thẳng AB có O là trung điểm. Vẽ hai đường thẳng m và n lần lượt vuông góc với AB tại A và B. Lấy điểm C trên m, CO cắt n tại D (Hình 24). Chứng minh rằng O là trung điểm CD.

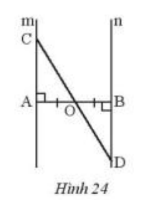
Lời giải: 

Xét (Delta OAC) và (Delta OBD), ta có:

(widehat {COA} = widehat {BOD}) ( 2 góc đối đỉnh)

AO = BO

(widehat A = widehat B)

(Rightarrow Delta OAC=Delta OBD) ( g-c-g )

( Rightarrow CO = DO) ( cạnh tương ứng )

( Rightarrow ) O là trung điểm CD

Bài 6 trang 58 sách giáo khoa Toán 7 Chân trời sáng tạo tập 2

Cho Hình 25 có EF = HG, EG = HF. Chứng minh rằng:

a) (Delta EFH=Delta HGE)

b) EF // HG

Lời giải: 

a) Xét tam giác EGH và tam giác HFE có :

FE = GH; GE = HF; EH chung

(Rightarrow Delta EFH=Delta HGE) (c-c-c)

( Rightarrow widehat {FEH} = widehat {EHG})( 2 góc tương ứng )

b) Vì (widehat {FEH}=widehat {EHG})

Mà 2 góc này ở vị trí so le trong

Do đó, EF // HG

Bài 7 trang 58 sách giáo khoa Toán 7 Chân trời sáng tạo tập 2

Cho tam giác FGH có FG = FH. Lấy điểm I trên cạnh GH sao cho FI là tia phân giác của (widehat {GFH}).Chứng minh rằng hai tam giác FIG và FIH bằng nhau.

Lời giải: 

Xét tam giác FIG và FIH có :

FI chung

FG = FH ( theo giả thiết )

(widehat {GFI} = widehat {HFI}) ( do FI là phân giác (widehat {GFH}))

(Rightarrow Delta FIG=Delta FIH) (c-g-c)

Bài 8 trang 58 sách giáo khoa Toán 7 Chân trời sáng tạo tập 2

Cho góc xOy. Lấy hai điểm A, B thuộc tia Ox sao cho OA

a) AD = BC

b) (Delta EAB=Delta ECD)

c) OE là tia phân giác của góc xOy.

Lời giải: 

a) Xét (Delta OAD) và (Delta OCB), ta có :

OD = OB

(widehat{A}) chung

OA = OC 

(Rightarrow Delta OAD=Delta OCB) (c-g-c )

( Rightarrow AD = BC)(2 cạnh tương ứng )

b) Vì (Delta OAD=Delta OCB) nên (widehat{OAD}=widehat{OCB}; widehat{D}=widehat{B}) ( 2 góc tương ứng)

Mà (widehat{OAD}+widehat{BAD}=180^0) ( 2 góc kề bù)

(widehat{OCB}+widehat{BCD}=180^0) ( 2 góc kề bù)

Do đó, (widehat{BAD}=widehat{BCD})

Vì (OA+AB=OB; OC+CD=OD)

Mà (OC = OA, OD = OB)

(Rightarrow AB=CD)

Xét (Delta EAB) và (Delta ECD), ta có:

(widehat {ABE} = widehat {CDE})

(AB = CD)

(widehat {BAE} = widehat {DCE})

(Rightarrow Delta EAB=Delta ECD) (g-c-g)

c) Vì (Delta EAB=Delta ECD) nên EB = ED ( 2 cạnh tương ứng)

Xét (Delta OBE) và (Delta ODE), ta có :

 EB = ED

OB = OD

OE chung

( Rightarrow Delta OBE=Delta ODE )  (c.c.c)

( Rightarrow widehat{BOE}=widehat{DOE}) ( 2 góc tương ứng)

( Rightarrow ) OE là phân giác (widehat {xOy})

Bài 9 trang 58 sách giáo khoa Toán 7 Chân trời sáng tạo tập 2

Đặt tên cho một số điểm có trong Hình 26 và chỉ ra ba cặp tam giác bằng nhau trong hình đó.

Lời giải: 

Đặt tên các điểm như hình trên.

Dựa vào hình trên ta có các cặp tam giác bằng nhau như sau:

∆ABC = ∆MNP; ∆ADC = ∆MQP; ∆ADC = ∆DEF.

Trường

Giải bài tập