Giải bài 1, 2, 3, 4, 5, 6, 7 trang 75 SGK Toán 7 tập 1 – CTST

Giải bài tập trang 75 Bài 2 Tia phân giác sgk toán 7 tập 1 chân trời sáng tạo. Bài 3 Cho đường thẳng MN, PQ cắt nhau tại A Tính số đo các góc còn lại.

Bài 1 trang 75 sách giáo khoa Toán 7 Chân trời sáng tạo tập 1

a) Trong Hình 8, tìm tia phân giác của góc (widehat {ABC},widehat {ADC})

b) Cho biết (widehat {ABC} = 100^circ ;widehat {ADC} = 60^circ ). Tính số đo của các góc (widehat {ABO},widehat {ADO})

Bạn đang xem: Giải bài 1, 2, 3, 4, 5, 6, 7 trang 75 SGK Toán 7 tập 1 – CTST

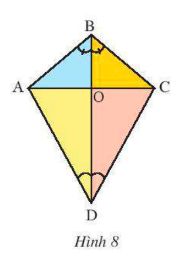
Lời giải:

a) Tia BO là tia phân giác của (widehat {ABC}) vì tia BO nằm giữa 2 tia BA và BC, tạo với 2 cạnh BA và BC 2 góc bằng nhau.

Tia DO là tia phân giác của (widehat {ADC}) vì tia DO nằm giữa 2 tia DA và DC, tạo với 2 cạnh DA và DC 2 góc bằng nhau

b) Vì BO là tia phân giác của (widehat {ABC}) nên (widehat {ABO} = widehat {CBO} = frac{1}{2}.widehat {ABC} = frac{1}{2}.100^circ  = 50^circ )

Vì DO là tia phân giác của (widehat {ADC})nên (widehat {ADO} = widehat {CDO} = frac{1}{2}.widehat {ADC} = frac{1}{2}.60^circ  = 30^circ )

Vậy (widehat {ABO} = 50^circ ;widehat {ADO} = 30^circ )

Bài 2 trang 75 sách giáo khoa Toán 7 Chân trời sáng tạo tập 1

a) Vẽ (widehat {xOy}) có số đo là 110 (^circ ).

b) Vẽ tia phân giác của (widehat {xOy}) trong câu a

Lời giải:

a) Các bước vẽ góc xOy có số đo 110 (^circ ).

Bước 1: Vẽ tia Ox bất kì. Ta đặt thước đo góc sao cho tâm của thước trùng với đỉnh O của góc.

Bước 2: Xoay thước sao cho một cạnh Ox của góc đi qua vạch 0 của thước và thước chồng lên phần trong của góc.

Bước 3: Tại vạch chỉ số 110 trên thước đo góc, chấm một chấm nhỏ. Nối điểm đó với điểm O.

Ta được góc xOy có số đo 110 (^circ ).

b)

Bài 3 trang 75 sách giáo khoa Toán 7 Chân trời sáng tạo tập 1

Cho đường thẳng MN, PQ cắt nhau tại A và tạọ thành (widehat {PAM} = 33^circ ) (Hình 9)

a) Tính số đo các góc còn lại.

b) Vẽ tia At là tia phân giác của (widehat {PAN}). Hãy tính số đo của (widehat {tAQ}). Vẽ At’ là tia đối của tia At. Giải thích tại sao At’ là tia phân giác của (widehat {MAQ})

Lời giải:

a) Ta có: (widehat {PAM} = widehat {QAN}) ( 2 góc đối đỉnh) , mà (widehat {PAM} = 33^circ )nên (widehat {QAN} = 33^circ )

Vì (widehat {PAN} + widehat {PAM} = 180^circ ) ( 2 góc kề bù) nên (widehat {PAN} + 33^circ  = 180^circ  Rightarrow widehat {PAN} = 180^circ  – 33^circ  = 147^circ )

Vì (widehat {PAN} = widehat {QAM})( 2 góc đối đỉnh) , mà (widehat {PAN} = 147^circ ) nên (widehat {QAM} = 147^circ )

b)

Vì At là tia phân giác của (widehat {PAN}) nên (widehat {PAt} = widehat {tAN} = frac{1}{2}.widehat {PAN} = frac{1}{2}.147^circ  = 73,5^circ )

Vì (widehat {tAQ} + widehat {PAt} = 180^circ ) ( 2 góc kề bù) nên (widehat {tAQ} + 73,5^circ  = 180^circ  Rightarrow widehat {tAQ} = 180^circ  – 73,5^circ  = 106,5^circ )

Vẽ At’ là tia đối của tia At, ta được (widehat {QAt’} = widehat {PAt})( 2 góc đối đỉnh)

Ta có: (widehat {QAt’} = widehat {MAt’} = frac{1}{2}.widehat {MAQ}) nên At’ là tia phân giác của (widehat {MAQ})

Chú ý:

2 tia phân giác của 2 góc đối đỉnh là 2 tia đối nhau

Bài 4 trang 75 sách giáo khoa Toán 7 Chân trời sáng tạo tập 1

Cho đường thẳng xy đi qua điểm O. Vẽ tia Oz sao cho (widehat {xOz} = 135^circ ). Vẽ tia Ot sao cho (widehat {yOt} = 90^circ ) và (widehat {zOt} = 135^circ ). Gọi Ov là tia phân giác của (widehat {xOt}). Các góc (widehat {xOv}) và (widehat {yOz}) có phải là hai góc đối đỉnh không? Vì sao?

Lời giải:

Vì (widehat {yOt} = 90^circ  Rightarrow Oy bot Ot Rightarrow Ox bot Ot) nên (widehat {xOt} = 90^circ )

Vì Ov là tia phân giác của (widehat {xOt}) nên (widehat {xOv} = widehat {vOt} = frac{1}{2}.widehat {xOt} = frac{1}{2}.90^circ  = 45^circ )

Vì (widehat {vOx} + widehat {xOz} = 45^circ  + 135^circ  = 180^circ ) nên Ov và Oz là hai tia đối nhau

Như vậy, các góc (widehat {xOv}) và (widehat {yOz}) là hai góc đối đỉnh vì Ox là tia đối của tia Oy, tia Ov là tia đối của tia Oz

Bài 5 trang 75 sách giáo khoa Toán 7 Chân trời sáng tạo tập 1

Vẽ hai góc kề bù (widehat {xOy},widehat {yOx’}), biết (widehat {xOy} = 142^circ ). Gọi Oz là tia phân giác của (widehat {xOy}). Tính (widehat {x’Oz})

Lời giải:

Bài 6 trang 75 sách giáo khoa Toán 7 Chân trời sáng tạo tập 1

Vẽ hai góc kề bù (widehat {xOy},widehat {yOx’}), biết (widehat {xOy} = 120^circ ). Gọi Oz là tia phân giác của (widehat {xOy}), Oz’ là tia phân giác của (widehat {yOx’}). Tính (widehat {zOy},widehat {yOz’},widehat {zOz’})

Lời giải:

Vì Oz là tia phân giác của (widehat {xOy}) nên (widehat {xOz} = widehat {zOy} = frac{1}{2}.widehat {xOy} = frac{1}{2}.120^circ  = 60^circ )

Vì Oz’ là tia phân giác của (widehat {yOx’}) nên (widehat {x’Oz’} = widehat {yOz’} = frac{1}{2}.widehat {yOx’} = frac{1}{2}.60^circ  = 30^circ )

Vì (widehat {zOy} + widehat {yOz’} = widehat {zOz’} Rightarrow 60^circ  + 30^circ  = widehat {zOz’} Rightarrow widehat {zOz’} = 90^circ )

Vậy (widehat {zOy} = 60^circ ,widehat {yOz’} = 30^circ ,widehat {zOz’} = 90^circ )

Chú ý:

2 tia phân giác của 2 góc kề bù thì vuông góc với nhau

Bài 7 trang 75 sách giáo khoa Toán 7 Chân trời sáng tạo tập 1

Vẽ góc bẹt (widehat {xOy}). Vẽ tia phân giác Oz của góc đó. Vẽ tia phân giác Ot của (widehat {xOz}). Vẽ tia phân giác Ov của (widehat {zOy}) . Tính (widehat {tOv})

Lời giải:

Vì Oz là tia phân giác của (widehat {xOy}) nên (widehat {xOz} = widehat {zOy} = frac{1}{2}.widehat {xOy}) = (frac{1}{2}.180^circ  = 90^circ )

Vì Ot là tia phân giác của (widehat {xOz}) nên (widehat {xOt} = widehat {tOz} = frac{1}{2}widehat {xOz} = frac{1}{2}.90^circ  = 45^circ )

Vì Ov là tia phân giác của (widehat {zOy}) nên (widehat {yOv} = widehat {vOz} = frac{1}{2}widehat {zOy} = frac{1}{2}.90^circ  = 45^circ )

Mà (widehat {tOz} + widehat {zOv} = widehat {tOv} Rightarrow 45^circ  + 45^circ  = widehat {tOv} Rightarrow widehat {tOv} = 90^circ )

Vậy (widehat {tOv} = 90^circ )

Trường

Giải bài tập