Giải bài 1, 2, 3, 4, 5, 6 trang 62, 63 SGK Toán 7 tập 2 – CTST

Giải bài tập trang 62, 63 Bài 3 Tam giác cân sgk toán 7 tập 2 chân trời sáng tạo. Bài 1 Tìm các tam giác cân và tam giác đều trong mỗi hình sau (Hình 13). Giải thích.

Bài 1 trang 62 sách giáo khoa Toán 7 Chân trời sáng tạo tập 2

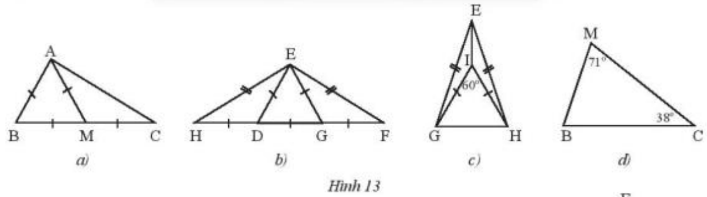
Tìm các tam giác cân và tam giác đều trong mỗi hình sau (Hình 13). Giải thích.

Bạn đang xem: Giải bài 1, 2, 3, 4, 5, 6 trang 62, 63 SGK Toán 7 tập 2 – CTST

Lời giải: 

a) Tam giác ABM là tam giác đều do có 3 cạnh bằng nhau

   Tam giác AMC cân tại M do AM = MC

b) Tam giác EDG là tam giác đều do có 3 cạnh bằng nhau

   Tam giác EHF cân tại E do EH = EF

   Tam giác EDH cân tại D do DH = DE

c) Tam giác EGF cân tại G do GE = GF

   Tam giác IHG đều do là tam giác cân có 1 góc = 60°

   Tam giác EHG cân tại E do EG = EH

d) Tam giác MBC không cân và không đều vì 3 góc có số đo khác nhau

Bài 2 trang 62 sách giáo khoa Toán 7 Chân trời sáng tạo tập 2

Cho Hình 14, biết ED = EF và EI là tia phân giác của (widehat {DEF})

Chứng minh rằng:

a) (Delta EID = Delta EIF)

b) Tam giác DIF cân

Lời giải: 

a) Xét tam giác EID và tam giác EIF có :

IE chung

ED = EF

(widehat {IED} = widehat {IEF})( EI là tia phân giác của (widehat {DEF}))

( Rightarrow Delta EID = Delta EIF(c – g – c))

b) Vì (Delta EID = Delta EIF) nên ID = IF ( 2 cạnh tương ứng )

Do đó tam giác DIF cân tại I (theo định nghĩa tam giác cân)

Bài 3 trang 63 sách giáo khoa Toán 7 Chân trời sáng tạo tập 2

Cho tam giác ABC cân tại A có (widehat A = {56^o})(Hình 15)

a) Tính(widehat B), (widehat C)

b) Gọi M, N lần lượt là trung điểm của AB, AC. Chứng minh rằng tam giác AMN cân.

c) Chứng minh rằng MN // BC

Lời giải:

a) Theo đề bài ta có tam giác ABC cân ở A và (widehat A = {56^o})

Mà ( Rightarrow widehat A + widehat B + widehat C = {180^o})

( Rightarrow widehat B = widehat C = ({180^o} – {56^o}):2 = {62^o})

b) Vì tam giác ABC cân tại A nên AB = AC ( định nghĩa tam giác cân )

Mà M, N là trung điểm của AB, AC

Nên AM = AN

Xét tam giác AMN có AM = AN nên AMN là tam giác cân tại A

( Rightarrow widehat M = widehat N = ({180^o} – {56^o}):2 = {62^o})

c) Vì (widehat {AMN}=widehat {ABC}) (cùng bằng 62°)

Mà chúng ở vị trí đồng vị nên MN⫽BC

Bài 4 trang 63 sách giáo khoa Toán 7 Chân trời sáng tạo tập 2

Cho tam giác ABC cân tại A (Hình 16). Tia phân giác của góc B cắt AC tại F, tia phân giác của góc C cắt AB tại E.

a) Chứng minh rẳng (widehat {ABF} = widehat {ACE})

b) Chứng minh rằng tam giác AEF cân

c) Gọi I là giao điểm của BF và CE. Chứng minh rằng tam giác IBC và tam giác IEF là những tam giác cân

Lời giải:

a) Vì tam giác ABC cân tại A

( Rightarrow widehat B = widehat C Rightarrow dfrac{1}{2}widehat B = dfrac{1}{2}widehat C Rightarrow widehat {ABF} = widehat {ACE})

b) Xét (Delta ECA) và (Delta FBA)có:

(widehat{A}) chung

AB = AC

(widehat {ABF} = widehat {ACE})

( Rightarrow )(Delta ECA)= (Delta FBA)( g – c – g )

( Rightarrow AE = AF và EC = BF) (2 cạnh tương ứng)

( Rightarrow Delta AEF) cân tại A

c) Xét tam giác IBC có :

(widehat B = widehat C Rightarrow dfrac{1}{2}widehat B = dfrac{1}{2}widehat C Rightarrow widehat {ICB} = widehat {IBC})

Do đó, tam giác IBC cân tại I ( 2 góc ở đáy bằng nhau )

( Rightarrow IB = IC)( cạnh tương ứng )

Vì EC = BF ( câu b) và IB = IC

( Rightarrow ) EC – IC = BF – BI

( Rightarrow ) EI = FI

( Rightarrow Delta IEF) cân tại I

Bài 5 trang 63 sách giáo khoa Toán 7 Chân trời sáng tạo tập 2

Phần thân của một móc treo quần áo có dạng hình tam giác cân (Hình 17a) được vẽ lại như Hình 17b. Cho biết AB = 20 cm; BC = 28 cm và (widehat B)= 35°. Tìm số đo các góc còn lại và chu vi của tam giác ABC.

Lời giải:

Vì tam giác ABC cân tại A

( Rightarrow ) AB = AC ( định lí tam giác cân ) = 20 cm

( Rightarrow ) Chu vi tam giác ABC = AB + AC + BC = 20 + 20 + 28 = 68 cm

Vì ABC là tam giác cân tại A ( Rightarrow widehat B = widehat C) ( 2 góc ở đáy ) = 35°

Mà theo định lí tổng 3 góc trong tam giác = 180°

( Rightarrow widehat A = {180^o} – widehat B – widehat C = {180^o} – {35^o} – {35^o} = {110^o})

Bài 6 trang 63 sách giáo khoa Toán 7 Chân trời sáng tạo tập 2

Một khung cửa sổ hình tam giác có thiết kế như Hình 18a được vẽ lại như Hình 18b.

a) Cho biết (widehat {{A_1}})( = {42^o}). Tính số đo của (widehat {{M_1}}),(widehat {{B_1}}),(widehat {{M_2}}).

b) Chứng minh MN // BC, MP // AC.

c) Chứng minh bốn tam giác cân AMN, MBP, PMN, NPC bằng nhau.

Lời giải:

a)      Ta thấy tam giác AMN cân tại A do AM = AN

( Rightarrow widehat {{M_1}} = ({180^o} – widehat {{A_1}}):2 = ({180^o} – {42^o}):2 = {69^o})

Ta thấy tam giác PMN = tam giác AMN ( c-c-c )

( Rightarrow widehat {{M_1}} = widehat {PMN} = {69^o}) (góc tương ứng )

Mà ( Rightarrow widehat {{M_1}} + widehat {{M_2}} + widehat {PMN} = {180^o})( các góc kề bù )

( Rightarrow widehat {{M_2}} = {180^o} – {69^o} – {69^o} = {42^o})

Mà tam giác MPB cân tại M do MB = MP nên

( Rightarrow widehat {{B_1}} = widehat {MPB})

Áp dụng định lí tổng 3 góc trong tam giác

( Rightarrow widehat {{B_1}} = ({180^o} – {42^o}):2 = {69^o})

b)      Ta thấy (widehat {{B_1}})và (widehat {{M_1}})ở vị trí đồng vị và bằng nhau nên

( Rightarrow )MN⫽BC

Vì tam giác PMN = tam giác AMN nên ta có

( Rightarrow widehat {{M_1}} = widehat {ANM} = widehat {PMN} = widehat {MNP})( do 2 tam giác cân và bằng nhau )

Mà (widehat {MNA})và(widehat {PMN}) ở vị trí so le trong

( Rightarrow )MP⫽AC

c)      Ta có (Delta AMN = Delta PMN = Delta MBP(c – g – c))(1)

Vì MP⫽AC ( chứng minh trên )

( Rightarrow widehat {MPN} = widehat {PNC}) ( 2 góc so le trong ) =({42^o})

( Rightarrow Delta MPN = Delta NCP(c – g – c))(2)

Từ (1) và (2) ( Rightarrow ) 4 tam giác cân AMN, MBP, PMN, NCP bằng nhau 

Trường

Giải bài tập