Giải bài 11, 12, 13, 14 trang 63, 64 SGK toán 8 tập 2

Giải bài tập trang 63 bài 2 Định lí đảo và hệ quả của định lí Talet Sách giáo khoa toán 8 tập 2. Câu 11: Tam giác ABC có BC= 15cm…

Bài 11 trang 63 – Sách giáo khoa toán 8 tập 2

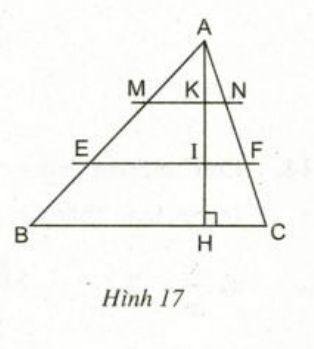
Tam giác ABC có BC= 15cm. Trên đường cao AH lấy các điểm I,K sao cho AK = KI = IH. Qua I và K vẽ các đường EF // BC, MN // BC(h.17)

a) Tính độ dài đoạn MN và EF.

Bạn đang xem: Giải bài 11, 12, 13, 14 trang 63, 64 SGK toán 8 tập 2

b) Tính diện tích tứ giác MNFE, biết diện tích của tam giác ABC là 270 cm²

Giải:

a) 

∆ABC có MN // BC.

=> (frac{MN}{CB}) = (frac{AK}{AH})(kết quả bài tập 10)

Mà AK = KI = IH

Nên (frac{AK}{AH}) = (frac{1}{3}) => (frac{MN}{CB}) = (frac{1}{3}) => MN = (frac{1}{3})BC = (frac{1}{3}).15 = 5 cm.

∆ABC có EF // BC => (frac{EF}{BC}) = (frac{AI}{AH}) = (frac{2}{3})

=> EF = (frac{2}{3}).15 =10 cm.

b) Áp dụng kết quả ở câu b của bài 10 ta có:

S_AMN= (frac{1}{9}).S_ABC= 30 cm²

S_AEF= (frac{4}{9}).S_ABC= 120 cm²

Do đó SMNEF = S_AEF – S_AMN = 90 cm²

Bài 12 trang 64 – Sách giáo khoa toán 8 tập 2

Có thể đo dược chiều rông của một khúc sông mà không cần phải sang bờ bên kia hay không?

Người ta tiền hành đo đạc các yếu tố hình học cần thiết để tình chiều rộng của khúc sông mà không cần phải sang bờ bên kia(h18). Nhìn hình vẽ, Hãy mô tả những công việc cần làm và tính khoảng cách AB=x theo BC=a a, B’C’= a’, BB’= h.

Giải: mô tả cách làm:

* Chọn một điểm A cố định bên mép bờ sông bên kia( chẳng hạn như là một thân cây), đặt hai điểm B và B’ thẳng hàng với A, điểm B sát mép bờ còn lại và AB chình là khoảng cách cần đo.

* Trên hai đường thẳng vuông góc với AB’ tại B và B’ lấy C và C’ thẳng hàng với A.

* Đo độ dài các đoạn BB’= h, BC= a, B’B’= a’.

Giải

Ta có:

(frac{AB}{AB’}) = (frac{BC}{BC’}) mà AB’ = x + h nên 

(frac{x}{x+ h}) = (frac{a}{a’})  a’x = ax + ah

a’x – ax = ah

x(a’ – a) = ah

x= (frac{ah}{a’-a})

Vậy khoảng cách AB bằng (frac{ah}{a’-a})

Bài 13 trang 64 – Sách giáo khoa toán 8 tập 2

Có thể đo gián tiếp chiều cao của một bức tường bằng dụng cụ do đơn giản được không?

Hình 19: thể hiện cách đo chiều cao AB của một bức tường bằng các dụng cụ đơn giản gồm:

Hai cọc thẳng đứng và sợi dây FC, Cọc 1 có chiều cao DK= h. Các khoảng cách BC= a, DC= b đo được bằng thước thông dụng.

a) Em hay cho biết người ta tiến hành đo đạc như thế nào ? 

b) Tính chiều cao AB theo h, a, b.

a) Cách tiến hành:

– Đặt hai cọc thẳng đứng, di chuyển cọc 2 sao cho 3 điểm A,F,K nằm trên đường thẳng.

– Dùng sợi dây căng thẳng qua 2 điểm F và K để xác định điểm C trên mặt đất( 3 điểm F,K,C thẳng hàng).

b) ∆BC có AB // EF nên (frac{EF}{AB}) = (frac{EC}{BC}) => AB = (frac{EF.BC}{EC}) = (frac{h.a}{b})

Vậy chiều cao của bức tường là: AB = (frac{h.a}{b}).

Bài 14 trang 64 – Sách giáo khoa toán 8 tập 2

Cho ba đoạn thẳng có độ dài là m,n,p( cùng đơn vị đo).

Dựng đoạn thẳng có độ dài x sao cho:

a) (frac{x}{m})= 2;     b) (frac{x}{n}) = (frac{2}{3});       c) (frac{m}{x}) = (frac{n}{p})

Giải: 

a) Cách dựng:

– Vẽ hai tia Ox, Oy không đối nhau.

– Trên tia Oy đặt điểm B sao cho OB = 2 đơn vị.

– Lấy trung điểm của OB,

– Nối MA.

– Vẽ đường thẳng đi qua B và song song với MA cắt Ox tại C thì (frac{OC}{OA}) = (frac{OB}{OM}); OB = 2 OM

=> (frac{x}{m}) = 2

b) Cách dựng:

– Vẽ hai tia Ox và Oy không đối nhau.

– Trên tia Ox đặt hai đoạn OA= 2 đơn vị, OB= 3 đơn vị.

– Trên tia Oy đặt đoạn OB’ = n

– Nối BB’

– Vẽ đường thẳng qua A song song với BB’ cắt Oy tại A’ và OA’ = x.

Ta có: AA’ // BB’ => (frac{OA’}{OB’}) = (frac{OA}{OB})

hay (frac{x}{n}) = (frac{2}{3})

c) Cách dựng:

– Vẽ tia Ox, Oy không đối nhau.

– Trên tia Ox đặt đoạn OA= m, OB= n.

– Trên tia Oy đặt đoạn OB’ = p.

– Vẽ đường thẳng qua A và song song với BB’ cắt Oy tại A’ thì OA’ = x.

Thật vậy: AA’ // BB’ => (frac{OA}{x}) = (frac{OB}{OB’}) hay (frac{m}{x}) = (frac{n}{p})

Trường

Giải bài tập