Giải bài 114, 115, 116, 117 trang 94 SBT Toán 8 tập 1

Giải bài tập trang 94 bài 9 hình chữ nhật Sách bài tập (SBT) Toán 8 tập 1. Câu 114: Cho tam giác ABC vuông cân tại A, AC = 4cm, điểm M thuộc cạnh BC. Gọi D, E theo thứ tự là chân các đường vuông góc kẻ từ M đến AB, AC….

Câu 114 trang 94 Sách bài tập (SBT) Toán 8 tập 1

Cho tam giác ABC vuông cân tại A, AC = 4cm, điểm M thuộc cạnh BC. Gọi D, E theo thứ tự là chân các đường vuông góc kẻ từ M đến AB, AC.

a. Tứ giác ADME là hình gì ? Tính chu vi của tứ giác đó.

Bạn đang xem: Giải bài 114, 115, 116, 117 trang 94 SBT Toán 8 tập 1

b. Điểm M ở vị trí nào trên cạnh BC thì đoạn thẳng DE có độ dài nhỏ nhất ?

Giải:                                                                   

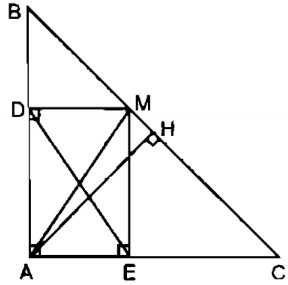
a. Xét tứ giác ADME ta có:

(widehat A = {90^0}) (gt)

MD ⊥ AB (gt)

( Rightarrow widehat {ADM} = {90^0})

ME ⊥ AC (gt)

( Rightarrow widehat {AEM} = {90^0})

Suy ra: Tứ giác ADME là hình chữ nhật (vì có ba góc vuông)

∆ ABC vuông cân tại A ( Rightarrow widehat B = {45^0})

Suy ra: ∆ DBM vuông cân tại D ⇒ DM = DB

Chu vi hình chữ nhật ADME bằng :

2(AD + DM) = 2 ( AD + DB) = 2 AB = 2.4 = 8 (cm)

b. Gọi H là trung điểm của BC

Suy ra: AH ⊥ BC (tính chất tam giác cân)

AM ≥ AH (dấu “=” xảy ra khi M trùng với H)

Tứ giác ADME là hình chữ nhật

⇒ AM = DE (tính chất hình chữ nhật)

Suy ra: DE ≥ AH

Vậy DE  = AH có độ dài nhỏ nhất khi điểm M là trung điểm của BC.

Câu 115 trang 94 Sách bài tập (SBT) Toán 8 tập 1

Cho tam giác ABC cân tại A, các đường trung tuyến BM, CN cắt nhau tại G. Gọi D là điểm đối xứng với G qua M, gọi E là điểm đối xứng với G qua N. Tứ giác BEDC là hình gì ? Vì sao ?

Giải:                                                                     

Ta có: G là trọng tâm của ∆ ABC

⇒ GB = 2GM (tính chất đường trung tuyến)

GC = 2GN (tính chất đường trung tuyến)

Điểm D đối xứng với điểm G qua điểm M

⇒ MG = MD hay GD = 2 GM

Suy ra: GD = GD (1)

Điểm E đối xứng với điểm G qua điểm N

⇒ NG = NE hay GE = 2 GN

Suy ra: GC = GE (2)

Từ (1) và (2) suy ra tứ giác BCDE là hình bình hành (vì có hai đường chéo cắt nhau tại trung điểm mỗi đường)

Xét ∆ BCM và ∆ CBN:

BC cạnh chung

(widehat {BCM} = widehat {CBN}) (tính chất tam giác cân)

CM = BN ( vì AB = AC)

Do đó: ∆ BCM = ∆ CBN (c.g.c)

( Rightarrow {widehat B_1} = {widehat C_1})⇒ ∆ GBC cân tại G ⇒ GB = GC ⇒ BD = CE

Hình bình hành BCDE có hai đường chéo bằng nhau là hình chữ nhật.

Câu 116 trang 94 Sách bài tập (SBT) Toán 8 tập 1

Cho hình chữ nhật ABCD. Gọi H là chân đường vuông góc kẻ từ A đến BD. Biết HD = 2cm, HB = 6cm. Tính các độ dài AD, AB (làm tròn đến hàng đơn vị).

Giải:                                                                   

Ta có: DB = HD + HB = 2 + 6 = 8(cm)

AC = DB (tính chất hình chữ nhật)

OA = OB = OC = OD = ({1 over 2})BD = 4(cm)

OD = OH + HD

⇒ OH = OD – HD = 4 – 2 = 2(cm)

AH ⊥ OD có HO = HD = 2(cm)

Suy ra: ∆ ADO cân tại A

⇒ AD = AO = 4(cm)

Trong tam giác vuông ABD có (widehat {BAD} = {90^0})

(B{D^2} = A{B^2} + A{D^2}) (định lý Pi-ta-go) ( Rightarrow A{B^2} = B{D^2} – A{D^2})

(AB = sqrt {B{D^2} – A{D^2}}  = sqrt {{8^2} – {4^2}}  = sqrt {48}  approx 7) (cm).

Câu 117 trang 94 Sách bài tập (SBT) Toán 8 tập 1

Chứng minh rằng ba điểm C, B, D trên hình 18 thẳng hàng.

Giải:                                                                          

Nối AB, BO, BC, BO’, BD.

Trong ∆ ABC ta có:

OA = OC = R (bán kính đường tròn (O))

nên BO là đường trung tuyến của ∆ ABC

mà BO = R(bán kính (O))

⇒ BO = OA = OC = ({1 over 2})AC

nên tam giác ABC vuông tại B ( Rightarrow widehat {ABC} = {90^0})

Trong ∆ ABD ta có: AO’ = O’D = R’ (bán kính (O’))

nên BO’ là đường trung tuyến của ∆ ABD

mà BO’ = R’ (bán kính (O’)) ⇒ BO’ = AO’ = O’D = ({1 over 2})AD

nên tam giác ABD vuông tại B ( Rightarrow widehat {ABD} = {90^0})

(widehat {ABC} + widehat {ABD} = widehat {CBD})

( Rightarrow widehat {CBD} = {90^0} + {90^0} = {180^0})

Vậy C, B, D thẳng hàng.

Trường

Giải bài tập