Giải bài 151, 152, 153 trang 98, 99 SBT Toán 8 tập 1

Giải bài tập trang 98, 99 bài 12 hình vuông Sách bài tập (SBT) Toán 8 tập 1. Câu 151: Cho hình vuông ABCD. Gọi E là một điểm nằm giữa C và D…

Câu 151 trang 98 Sách bài tập (SBT) Toán 8 tập 1

Cho hình vuông ABCD. Gọi E là một điểm nằm giữa C và D. Tia phân giác của góc DAE cắt CD ở F. Kẻ FH ⊥ AE (H ∈ AE), FH cắt BC ở G.

Tính số đo góc FAG.

Bạn đang xem: Giải bài 151, 152, 153 trang 98, 99 SBT Toán 8 tập 1

Giải:                                                           

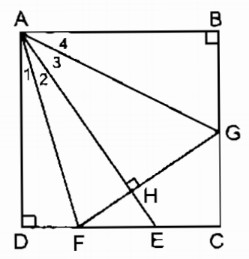
Xét hai tam giác vuông DAF và HAF:

(widehat {ADF} = widehat {AHF} = {90^0})

({widehat A_1} = {widehat A_2}) (gt)

AF cạnh huyền

Do đó: ∆ DAF = ∆ HAF (cạnh huyền, góc nhọn)

⇒ DA = HA

DA = AB (gt)

Suy ra: HA = AB

Xét hai tam giác vuông HAG và BAG:

(widehat {AHG} = widehat {ABG} = {90^0})

HA = BA (chứng minh trên)

AG cạnh huyền chung

Do đó: ∆ HAG = ∆ BAG (cạnh huyền, cạnh góc vuông)

( Rightarrow {widehat A_3} = {widehat A_4})nên AG là tia phân giác của (widehat {EAB})

(widehat {FAG} = {widehat A_2} + {widehat A_3} = {1 over 2}left( {widehat {DAE} + widehat {EAB}} right) = {1 over 2}{.90^0} = {45^0})

 

---

Câu 152 trang 99 Sách bài tập (SBT) Toán 8 tập 1

Cho hình vuông DEBC. Trên cạnh CD lấy điểm A, trên tia đối của tia DC lấy điểm K, trên tia đối tia ED lấy điểm M sao cho CA = DK = EM. Vẽ hình vuông DKIH (H thuộc cạnh DE). Chứng minh rằng ABMI là hình vuông.

Giải:                                                                 

Xét ∆ CAB và ∆ EMB :

CA = ME (gt)

(widehat C = widehat E = {90^0})

CB = EB (tính chất hình vuông)

Do đó: ∆ CAB = ∆ EMB (c.g.c)

⇒ AB = MB (1)

AK = DK +DA

CD = CA + AD

mà CA = DK nên AK = CD

Xét ∆ CAB và ∆ KIA :

CA = KI (vì cùng bằng DK)

(widehat C = widehat K = {90^0})

CB = AK (vì cùng bằng CD)

Do đó: ∆ CAB = ∆ KIA (c.g.c)

⇒ AB = AI (2)

DH = DK (vì KDHI là hình vuông)

EM = DK (gt)

⇒ DH + HE = HE + EM

hay DE = HM

Xét ∆ HIM và ∆ EMB :

HI = EM (vì cùng bằng DK)

(widehat H = widehat E = {90^0})

HM = EB (vì cùng bằng DE)

Do đó: ∆ HIM = ∆ EMB (c.g.c)

⇒ IM = MB (3)

Từ (1), (2) và (3) suy ra: AB = BM = AI = IM

Tứ giác ABMI là hình thoi.

Mặt khác, ta có ∆ ACB = ∆ MEB (chứng minh trên)

(eqalign{  &  Rightarrow widehat {CBA} = widehat {EBM}  cr  & widehat {CBA} + widehat {ABE} = widehat {CBE} = {90^0} cr} )

Suy ra: (widehat {EBM} + widehat {ABE} = {90^0}) hay (widehat {ABM} = {90^0})

Vậy : Tứ giác ABMI là hình vuông.

 

---

Câu 153 trang 99 Sách bài tập (SBT) Toán 8 tập 1

Cho tam giác ABC. Vẽ ở ngoài tam giác các hình vuông ABDE, ACFH.

a. Chứng minh rằng EC = BH, EC ⊥ BH.

b. Gọi M, N theo thứ tự là tâm của các hình vuông ABDE, ACFH. Gọi I là trung điểm của BC. Tam giác MIN là tam giác gì ? Vì sao ?

Giải:                                                                         

a. Ta có: (widehat {BAH} = widehat {BAC} + widehat {CAH} = widehat {BAC} + {90^0})

(widehat {EAC} = widehat {BAC} + widehat {BAE} = widehat {BAC} + {90^0})

Suy ra: (widehat {BAH} = widehat {EAC})

– Xét ∆ BAH và ∆ EAC:

BA = EA (vì ABDE là hình vuông)

(widehat {BAH} = widehat {EAC}) (chứng minh trên)

AH = AC (vì ACFH là hình vuông)

Do đó: ∆ BAH = ∆ EAC (c.g.c)

⇒ BH = EC

Gọi giao điểm của EC với AB và BH lần lượt là K và O.

(widehat {AEC} = widehat {ABH}) (vì ∆ BAH = ∆ EAC) (1)

hay (widehat {AEK} = widehat {OBK})

– Trong ∆ AEK ta có: (widehat {EAK} = {90^0})

( Rightarrow widehat {AEK} + widehat {AKE} = {90^0}) (2)

(widehat {AKE} = widehat {OKB}) (đối đỉnh) (3)

Từ (1) và (2) suy ra: (widehat {OKB} + widehat {OBK} = {90^0})

– Trong ∆ BOK ta có: (widehat {BOK} + widehat {OKB} + widehat {OBK} = {180^0})

( Rightarrow widehat {BOK} = {180^0} – left( {widehat {OKB} + widehat {OBK}} right) = {180^0} – {90^0} = {90^0})

Suy ra: EC ⊥ BH

b. Trong ∆ EBC ta có:

M là trung điểm của EB (tính chất hình vuông)

I là trung điểm của BC (gt)

nên MI là đường trung bình của tam giác EBC

⇒ MI = ({1 over 2})EC và MI // EC (tính chất đường trung bình của tam giác)

– Trong ∆ BCH ta có:

I là trung điểm của BC (gt)

N là trung điểm của CH (tính chất hình vuông)

nên NI là đường trung bình của ∆ BCH

⇒ NI = ({1 over 2})BH và NI // BH (tính chất đường trung bình của tam giác)

BH = CE (chứng minh trên)

Suy ra: MI = NI nên ∆ INM cân tại I

MI // EC (chứng minh trên)

EC ⊥ BH (chứng minh trên)

Suy ra: MI ⊥ BH

NI // BH (chứng minh trên)

Suy ra: MI ⊥ NI hay (widehat {MIN} = {90^0})

Vậy ∆ IMN vuông cân tại I.

Trường

Giải bài tập