Giải bài 157, 158, 159, 160 trang 99, 100 SBT Toán 8 tập 1

Giải bài tập trang 99, 100 bài ôn tập chương I – tứ giác Sách bài tập (SBT) Toán 8 tập 1. Câu 157: Cho tứ giác ABCD. Gọi E, F, G, H theo thứ tự là trung điểm của AB, BC, CD, DA. Tìm điều kiện của tứ giác ABCD để EFGH là…

Câu 157 trang 99 Sách bài tập (SBT) Toán 8 tập 1

Cho tứ giác ABCD. Gọi E, F, G, H theo thứ tự là trung điểm của AB, BC, CD, DA. Tìm điều kiện của tứ giác ABCD để EFGH là:

a. Hình chữ nhật

Bạn đang xem: Giải bài 157, 158, 159, 160 trang 99, 100 SBT Toán 8 tập 1

b. Hình thoi

c. Hình vuông

Giải:

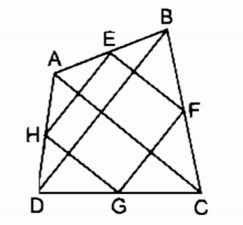
Trong ∆ ABC ta có EF là đường trung bình nên EF // AC và EF = ({1 over 2})AC (1)

Trong ∆ ADC ta có HG là đường trung bình nên HG // AC và HG = ({1 over 2})AC (2)

Từ (1) và (2) suy ra: EF // HG và EF = HG

Vậy tứ giác EFGH là hình bình hành

a. Tứ giác EFGH là hình chữ nhật ⇔ EH ⊥ EF ⇔ AC ⊥ BD

b. Tứ giác EFGH là hình thoi ⇔ EH = EF ⇔ AC = BD

c. Tứ giác EFGH là hình vuông ⇔ AC ⊥ BD và AC = BD

Câu 158 trang 100 Sách bài tập (SBT) Toán 8 tập 1

Cho tam giác ABC vuông tại A, điểm D là trung điểm của BC. Gọi M là điểm đối xứng với D qua AB, E là giao điểm của DM và AB. Gọi N là điểm đối xứng với D qua AC, F là giao điểm của DN và AC.

a. Tứ giác AEDF là hình gì ? Vì sao ?

b. Các tứ giác ADBM, ADCN là hình gì ? Vì sao ?

c. Chứng minh rằng M đối xứng với N qua A

d. Tam giác vuông ABC có điều kiện gì thì tứ giác AEDF là hình vuông ?

Giải:

a. Điểm M và điểm D đối xứng qua trục AB

⇒ AB là đường trung trực của đoạn thẳng MD

⇒ AB ⊥ DM

⇒ (widehat {AED} = {90^0})

Điểm D và điểm N đối xứng nhau qua trục AC ⇒ AC là đường trung trực của đoạn thẳng DN

⇒ AC ⊥ DN ( Rightarrow widehat {AFD} = {90^0})

(widehat {EAF} = {90^0}) (gt)

Vậy tứ giác AEDF là hình chữ nhật (vì có ba góc vuông)

b. Tứ giác AEDF là hình chữ nhật ⇒ DE // AC; DF // AB

Trong ∆ ABC ta có: DB = DC (gt)

DE // AC

Suy ra: AE = EB (tính chất đường trung bình tam giác); DF// AB

Suy ra: AF = FC (tính chất đường trung bình của tam giác)

Xét tứ giác ADBM : AE = EB (chứng minh trên)

ED = EM (vì AB là trung trực DM)

Suy ra: Tứ giác ADBM là hình bình hành (vì có hai đường chéo cắt nhau tại trung điểm mỗi đường)

AB ⊥ DM

Vậy hình bình hành ADBM là hình thoi ( vì có hai đường chéo vuông góc)

Xét tứ giác ADCN:

AF = FC (chứng minh trên)

DF = FN (vì AC là đường trung trực DN)

Suy ra: Tứ giác ADCN là hình bình hành (vì có hai đường chéo cắt nhau tại trung điểm mỗi đường)

AC ⊥ DN

Vậy hình bình hành ADCN là hình thoi (vì có hai đường chéo vuông góc)

c. Tứ giác ADBM là hình thoi ⇒ AM // DB và AM = AD

hay AM // BC và AM = AD (1)

Tứ giác ADCN là hình thoi ⇒ AN // DC và AD = AN

hay AN // BC và AN = AD (2)

Từ (1) và (2) suy ra: AM trung với AN hay M, A, N thẳng hàng

Và AM = AN nên A là trung điểm của MN

Vậy điểm M và điểm N đối xứng với nhau qua điểm A

d. Hình chữ nhật AEDF trở thành hình vuông khi AE = AF

Ta có: AE = ({1 over 2})AB ; AF =({1 over 2})AC

nên AE = AF AB = AC

Vậy nếu ∆ ABC vuông cân tại A thì tứ giác AEDF là hình vuông.

Câu 159 trang 100 Sách bài tập (SBT) Toán 8 tập 1

Cho tam giác ABC vuông tại A, đường cao AH. Gọi D là điểm đối xứng với H qua AB, gọi E là điểm đối xứng với H qua AC.

a. Chứng minh rằng D đối xứng với E qua A

b. Tam giác DHE là tam giác gì ? Vì sao ?

c. Tứ giác BDEC là hình gì ? Vì sao ?

d. Chứng minh rằng BC = BD + CE.

Giải:

a. Điểm D đối xứng điểm H qua trục AB

⇒ AB là đường trung trực của HD

⇒ AH = AD (tính chất đường trung trực) ⇒ ∆ ADH cân tại A

Suy ra: AB là tia phân giác của (widehat {DAH} Rightarrow widehat {DAB} = {widehat A_1})

Điểm H và điểm E đối xứng qua trục AC

⇒ AC là đường trung trực của HE

⇒ AH = AE (tính chất đường trung trực) ⇒ ∆ AHE cân tại A

Suy ra: AC là đường phân giác của (widehat {HAE} Rightarrow {widehat A_2} = widehat {EAC})

(widehat {DAE} = widehat {DAH} + widehat {HAE} = 2left( {{{widehat A}_1} + {{widehat A}_2}} right) = {2.90^0} = {180^0})

D, A, E thẳng hàng

AD = AE (vì cùng bằng AH)

nên điểm A là trung điểm của đoạn DE

Vậy điểm D đối xứng với điểm E qua điểm A.

b) Tam giác DHE có HA là trung tuyến và (AH = {1 over 2}DE)
nên tam giác DHE vuông tại H.

c) Xét (Delta ADB) và ( Delta AHB) có:

+) AB chung

+) BD = BH ( vì AB là trung trực của DH)

+) AD = AH (vì AB là trung trực của DH)

(Rightarrow Delta ADB = Delta AHB;(c.c.c))

( Rightarrow widehat {AHB} = widehat {ADB}=90^0) (hai góc tương ứng)

Xét (Delta AEC) và ( Delta AHC) có:

+) AC chung

+) EC = HC ( vì AC là trung trực của EH)

+) AE = AH (vì AC là trung trực của EH)

(Rightarrow Delta AEC = Delta AHC;(c.c.c))

( Rightarrow widehat {AHC} = widehat {AEC}=90^0) (hai góc tương ứng)

Suy ra BD//CE (vì cùng vuông góc với DE)
Do đó tứ giác BDEC là hình thang có 2 góc vuông kề cạnh bên DE nên BDEC là hình thang vuông.

d) Do AB là đường trung trực của DH nên BD=BH (5)
Do AC là đường trung trực của EH nên CE=CH (6)
Cộng vế với vế của (5) và (6) ta có BD+CE=BH+CH hay BD+CE=BC

Câu 160 trang 100 Sách bài tập (SBT) Toán 8 tập 1

Cho tứ giác ABCD. Gọi E, F, G, H theo thứ tự là trung điểm của AB, AC, DC, DB. Tìm điều kiện của tứ giác ABCD để EFGH là:

a. Hình chữ nhật

b. Hình thoi

c. Hình vuông

Giải: