Giải bài 19, 20, 21 trang 158 SBT Toán 8 tập 1

Giải bài tập trang 158 bài 2 diện tích hình chữ nhật Sách bài tập (SBT) Toán 8 tập 1. Câu 19: Tính diện tích các hình trên hình 182 (mỗi ô vuông là một đơn vị diện tích )…

Câu 19 trang 158 Sách bài tập (SBT) Toán 8 tập 1

Tính diện tích các hình trên hình 182 (mỗi ô vuông là một đơn vị diện tích ).

Hãy giải thích vì sao được tính như vậy.

Bạn đang xem: Giải bài 19, 20, 21 trang 158 SBT Toán 8 tập 1

Giải:                                                              

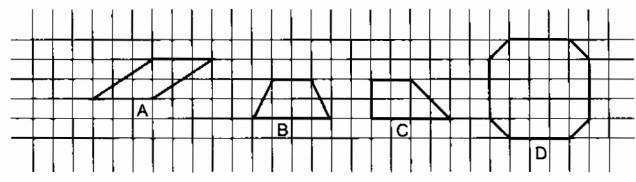
Hình A cắt rời hai thành tam giác ghép lại được một hình chữ nhật có một cạnh 3 ô vuông và một cạnh 2 ô vuông nên có diện tích 6 ô vuông (6 đơn vị diện tích)

Hình B là một hình thang cân, cắt theo đường cao kẻ từ một đỉnh của đáy nhỏ ghép lại ta được một hình chữ nhật có cạnh 3 ô vuông và một cạnh 2 ô vuông nên diện tích bằng 6 ô vuông (6 đơn vị diện tích)

Hình C là hình thang vuông, cắt phần nhọn ghép lên ta được một hình chữ nhật có một cạnh là 3 ô vuông và một cạnh 2 ô vuông nên diện tích bằng 6 ô vuông (6 đơn vị diện tích)

Hình D ta lấy diện tích hình vuông có cạnh 5 ô vuông trừ đi phần khuyết của 4 góc mỗi góc là một nửa ô vuông ta có diện tích là 5 x 5 – 4 . = 25 – 2 = 23 ô vuông (23 đơn vị diện tích).

Câu 20 trang 158 Sách bài tập (SBT) Toán 8 tập 1

Trên giấy kẻ ô vuông, hãy vẽ:

a. Hai hình chữ nhật có cùng chu vi nhưng khác diện tích.

b. Hai hình chữ nhật có kích thước khác nhau nhưng cùng diện tích.

Giải:

Hình vẽ sau đây                                   

Câu 21 trang 158 Sách bài tập (SBT) Toán 8 tập 1

Cho hình bình hành ABCD (h. 183). Từ A và C kẻ AH và CK vuông góc với đường chéo BD. Chứng minh rằng hai đa giác ABCH và ADCK có cùng diện tích.

Giải:                                                                   

Ta có: ∆ ABC = ∆ ADC (c.c.c)

( Rightarrow {S_{ABC}} = {S_{ADC}})  (1)

∆ AHC = ∆ AKC (c.c.c)

( Rightarrow {S_{AHC}} = {S_{AKC}}) (2)

Từ (1) và (2) suy ra:

({S_{ABC}} + {S_{AHC}} = {S_{ADC}} + {S_{AKC}})

hay ({S_{ABCH}} = {S_{ADCK}})

Trường

Giải bài tập