Giải bài 26, 27, 28, 29 trang 115, 116 SGK Toán 9 tập 1

Giải bài tập trang 115, 116 bài 6 tính chất của hai tiếp tuyến cắt nhau SGK Toán 9 tập 1. Câu 26: Cho đường tròn (O), điểm A nằm bên ngoài đường tròn. Kẻ các tiếp tuyến AB, AC với đường tròn (B, C là các tiếp điểm)…

Bài 26 trang 115 sgk Toán 9 – tập 1

Cho đường tròn (O), điểm A nằm bên ngoài đường tròn. Kẻ các tiếp tuyến AB, AC với đường tròn (B, C là các tiếp điểm).

a) Chứng minh rằng OA vuông góc với BC.

Bạn đang xem: Giải bài 26, 27, 28, 29 trang 115, 116 SGK Toán 9 tập 1

b) Vẽ đường kính CD. Chứng minh rằng BD song song với AO.

c) Tính độ dài các cạnh của tam giác ABC; biết (OB=2cm, OA=4cm).

Giải:

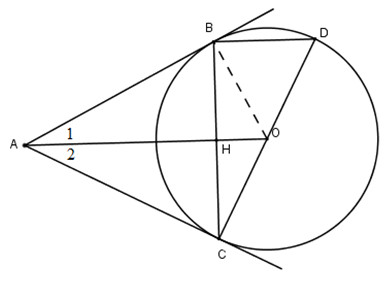
a) Vì AB, AC là các tiếp tuyến nên (AB=AC) và (widehat{A_{1}}=widehat{A_{2}}).

Suy ra (OAperp BC) (tính chất của tam giác cân).

b) Điểm B nằm trên đường tròn đường kính CD nên (widehat{CBD}=90^{circ}).

Suy ra BD//AO (vì cùng vuông góc với BC).

c) Nối OB thì (OBperp AB.)

Xét tam giác AOB vuông tại B có: (sin widehat {{A_1}} = {{OB} over {OA}}=frac{2}{4}=frac{1}{2})

(Rightarrow widehat{A_{1}}=30^{circ}Rightarrow widehat{BAC}=60^{circ}.)

Tam giác ABC cân, có một góc (60^{circ}) nên là tam giác đều.

Ta có (AB^{2}=OA^{2}-OB^{2}=4^{2}-2^{2}=12Rightarrow AB=2sqrt{3.})

Vậy (AB=AC=BC=2sqrt{3}cm).

Nhận xét. Qua câu c) ta thấy: Góc tạo bởi hai tiếp tuyến của một đường tròn vẽ từ một điểm cách tâm một khoảng bằng đường kính đúng bằng (60^{circ}).

Bài 27 trang 115 sgk Toán 9 – tập 1

Từ một điểm A nằm bên ngoài đường tròn (O), kẻ các tiếp tuyến AB, AC với đường tròn (B, C là các tiếp điểm). Qua điểm M thuộc cung nhỏ BC, kẻ tiếp tuyến với đường tròn O, nó cắt các tiếp tuyến AB và AC theo thứ tự ở D và E. Chứng minh rằng chu vi tam giác ADE bằng 2AB.

Hướng dẫn giải:

Theo tính chất hai tiếp tuyến cắt nhau ta có;

(AB=AC; ,,DB=DM;,,EC=EM.)

Chu vi (Delta ADE=AD + DM + ME + AE)

(= AD + DB + EC + AE)

(= AB + AC = 2AB)

Bài 28 trang 116 sgk Toán 9 – tập 1

Cho góc xAy khác góc bẹt. Tâm của các đường tròn tiếp xúc với hai cạnh của góc xAy nằm trên đường nào?

Giải:

Gọi O là tâm của một đường tròn bất kì tiếp xúc với hai cạnh góc xAy. Theo tính chất của hai tiếp tuyến cắt nhau ta có:

(widehat {xAO} = widehat {y{rm{A}}O})

Hay AO là tia phân giác của góc xAy. Vậy tâm O các đường tròn tiếp xúc với hai cạnh của góc xAy nằm trên tia phân giác của góc(xAy).

Bài 29 trang 116 sgk Toán 9 – tập 1

Cho góc xAy khác góc bẹt, điểm B thuộc Ax. Hãy dựng đường tròn (O) tiếp xúc với Ax tại B và tiếp xúc với Ay.

Giải:

Phân tích 

Đường tròn (O) tiếp xúc với hai cạnh của góc xAy nên tâm O nằm trên tia phân giác Am của góc xAy. Đường tròn (O) tiếp xúc với Ax tại B nên tâm O nằm trên đường thẳng (dperp Ax) tại B.

Vậy O là giao điểm của tia Am với đường thẳng d.

Cách dựng

– Dựng tia phân giác Am của góc xAy.

– Qua B dựng đường thẳng (dperp Ax), cắt tia Am tại O.

– Dựng đường tròn (O;OB), đó là đường tròn phải dựng.

Chứng minh

Vì (OBperp Ax) tại B nên đường tròn (O;OB) tiếp xúc với Ax tại B. 

Vì O nằm trên tia phân giác của góc xAy nên O cách đều hai cạnh của góc xAy. Do đó đường tròn (O;OB) tiếp xúc với Ay.

Biện luận. Bài toán luôn có một nghiệm hình.

Trường

Giải bài tập