Giải bài tập trang 111 bài 3 bảng lượng giác Sách bài tập (SBT) Toán 9 tập 1. Câu 39: Dùng bảng lượng giác hoặc máy tính bỏ túi để tìm…
Câu 39. Trang 111 Sách Bài Tập (SBT) Toán 9 Tập 1
Dùng bảng lượng giác hoặc máy tính bỏ túi để tìm:
(sin 39^circ 13’); (cos 52^circ 18’); (tg13^circ 20’);
Bạn đang xem: Giải bài 39, 40, 41, 42 trang 111 SBT Toán 9 tập 1
(cot g10^circ 17’); (sin 45^circ ); (cos 45^circ ).
Gợi ý làm bài:
(sin 39^circ 13′ approx 0,6323);
(cos 52^circ 18′ approx 0,6115);
(tg13^circ 20′ approx 0,2370);
(cot g10^circ 17′ approx 0,5118);
(sin 45^circ approx 0,7071);
(cos 45^circ approx 0,7071).
Câu 40. Trang 111 Sách Bài Tập (SBT) Toán 9 Tập 1
Dùng bảng lượng giác hoặc máy tính bỏ túi để tìm góc nhọn x, biết:
a) (sin x = 0,5446);
b) (cos x = 0,4444);
c) (tgx = 1,1111).
Gợi ý làm bài:
a) (sin x = 0,5446 Rightarrow x = 33^circ )
b) (cos x = 0,4444 Rightarrow x = 63^circ 47’)
c) (tg x = 1,1111 Rightarrow x = 48^circ )
Câu 41. Trang 111 Sách Bài Tập (SBT) Toán 9 Tập 1
Có góc nhọn x nào mà:
a) (sin x = 1,0100);
b) (cos x = 2,3540);
c) (tgx = 1,6754)?
Gợi ý làm bài:
a) (sin x = 1,0100): không có góc nhọn x vì (sin x
b) (cos x = 2,3540): không có góc nhọn x vì (cos x
c) (tgx = 1,6754 Rightarrow x = 59^circ 10’)
Câu 42. Trang 111 Sách Bài Tập (SBT) Toán 9 Tập 1
Cho hình:
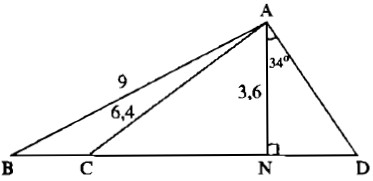
Biết:
(AB = 9cm,AC = 6,4cm)
(AN = 3,6cm,widehat {AN{rm{D}}} = 90^circ ,widehat {DAN} = 34^circ )
Hãy tính:
a) CN;
b) (widehat {ABN});
c) (widehat {CAN});
d) AD.
Gợi ý làm bài:
a) Áp dụng định lí Pi-ta-go vào tam giác vuông ANC, ta có:
(eqalign{
& A{C^2} = A{N^2} + N{C^2} cr
& Rightarrow N{C^2} = A{C^2} – A{N^2} cr
& Rightarrow NC = sqrt {A{C^2} – A{N^2}} = sqrt {6,{4^2} – 3,{6^2}} = sqrt {28} cr
& Rightarrow NC = 5,2915left( {cm} right) cr} )
b) Tam giác ANB vuông tại N nên ta có:
(sin widehat {ABN} = {{AN} over {AB}} = {{3,6} over 9} = 0,4)
( Rightarrow widehat {ABN} approx 23^circ 35’)
c) Tam giác ANC vuông tại N nên ta có:
(eqalign{
& cos widehat {CAN} = {{AN} over {AC}} cr
& Rightarrow {{3,6} over {6,4}} = {9 over {16}} = 0,5625 cr
& Rightarrow widehat {CAN} approx 55^circ 46′ cr} )
d) Tam giác AND vuông tại N nên ta có:
(eqalign{
& cos widehat {NAD} = {{AN} over {AD}} cr
& Rightarrow AD = {{AN} over {cos widehat {NAD}}} cr
& = {{3,6} over {cos 34^circ }} approx 4,3424 cr} )
Trường
Đăng bởi: Thcs-thptlongphu.edu.vn
Chuyên mục: Tổng hợp





