Giải bài 4.1, 4.2 trang 28 SBT Toán 8 tập 1

Giải bài tập trang 28 bài 4 quy đồng mẫu thức nhiều phân thức Sách bài tập (SBT) Toán 8 tập 1. Câu 4.1: Quy đồng mẫu thức ba phân thức…

Câu 4.1 trang 28 Sách bài tập (SBT) Toán 8 tập 1

Quy đồng mẫu thức ba phân thức

({x over {{x^2} – 2xy + {y^2} – {z^2}}}), ({y over {{y^2} – 2yz + {z^2} – {x^2}}}) , ({z over {{z^2} – 2zx + {x^2} – {y^2}}})

Bạn đang xem: Giải bài 4.1, 4.2 trang 28 SBT Toán 8 tập 1

Giải:

(eqalign{  & {x^2} – 2xy + {y^2} – {z^2} = {left( {x – y} right)^2} – {z^2} = left( {x – y + z} right)left( {x – y – z} right)  cr  & {y^2} – 2yz + {z^2} – {x^2} = left( {y – z + x} right)left( {y – z – x} right)  cr  &  =  – left( {x – y + z} right)left( {x + y – z} right)  cr  & {z^2} – 2xz + {x^2} – {y^2} = {left( {x – z} right)^2} – {y^2} = left( {x – z + y} right)left( {x – z – y} right) = left( {x + y – z} right)left( {x – y – z} right) cr} )

MTC =(left( {x – y + z} right)left( {x + y – z} right)left( {x – y – z} right))

(eqalign{  & {x over {{x^2} – 2xy + {y^2} – {z^2}}} = {x over {left( {x – y + z} right)left( {x – y – z} right)}} = {{xleft( {x + y – z} right)} over {left( {x – y + z} right)left( {x + y – z} right)left( {x – y – z} right)}}  cr  & {y over {{y^2} – 2yz + {z^2} – {x^2}}} = {y over {left( {y – z + x} right)left( {y – z – x} right)}} = {{ – y} over {left( {x – y + z} right)left( {x + y – z} right)}}  cr  &  = {{ – yleft( {x – y – z} right)} over {left( {x – y + z} right)left( {x + y – z} right)left( {x – y – z} right)}}  cr  & {z over {{z^2} – 2zx + {x^2} – {y^2}}} = {z over {left( {x + y – z} right)left( {x – y – z} right)}} = {{zleft( {x – y + z} right)} over {left( {x + y – z} right)left( {x – y + z} right)left( {x – y – z} right)}} cr} )

Câu 4.2 trang 28 Sách bài tập (SBT) Toán 8 tập 1

Cho hai phân thức ({1 over {{x^2} + ax – 2}}) , ({2 over {{x^2} + 5x + b}}). Hãy xác định a và b biết rằng khi quy đồng mẫu thức chúng trở thành những phân thức có mẫu thức chung là({x^3} + 4{x^2} + x – 6). Viết tường minh hai phân thức đã cho và hai phân thức thu được sau khi quy đồng với mẫu thức chung là ({x^3} + 4{x^2} + x – 6)

Giải:

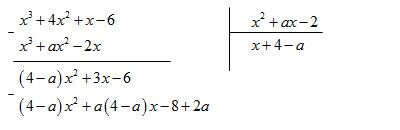
Vì phép chia này là phép chia hết nên số dư phải bằng 0

( Rightarrow aleft( {4 – a} right) = 3)  (1) và (2a – 8 =  – 6)  (2)

Từ (2) ( Rightarrow 2a – 8 =  – 6 Rightarrow a = 1)

a = 1 thỏa mãn (1) ta có phân thức ({1 over {{x^2} + x – 2}})

Vì phép chia này là phép chia hết nên số dư phải bằng 0

( Rightarrow left( {1 – b} right) = 5) (3) và – b = − 6 (4)

Từ (4) ⇒ − b = − 6 ⇒ b = 6

b = 6 thỏa mãn (3) ta có phân thức ({2 over {{x^2} + 5x + 6}})

(eqalign{  & {1 over {{x^2} + x – 2}} = {{left( {x + 3} right)} over {left( {{x^2} + x – 2} right)left( {x + 3} right)}} = {{x + 3} over {{x^3} + 4{x^2} + x – 6}}  cr  & {2 over {{x^2} + 5x + 6}} = {{2left( {x – 1} right)} over {left( {{x^2} + 5x + 6} right)left( {x – 1} right)}} = {{2x – 2} over {{x^3} + 4{x^2} + x – 6}} cr} )

Trường

Giải bài tập