Giải bài tập trang 36, 37, 38 bài 2 đồ thị của hàm số y = ax^2 (a≠0) SGK Toán 9 tập 2. Câu 4: Cho hai hàm số…
Bài 4 trang 36 sgk Toán 9 tập 2
Bài 4. Cho hai hàm số: (y = {3 over 2}{x^2},y = – {3 over 2}{x^2}). Điền vào những ô trống của các bảng sau rồi vẽ hai đồ thị trên cùng một mặt phẳng tọa độ.
Bạn đang xem: Giải bài 4, 5, 6 trang 36, 37, 38 SGK Toán 9 tập 2
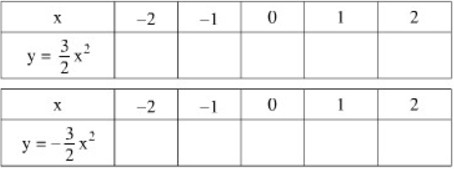
Nhận xét về tính đối xứng của hai đồ thị đối với trục Ox.
Bài giải:
Thực hiện phép tính và điền vào chỗ trống ta được bảng sau:

Vẽ đồ thị:

Nhận xét: Đồ thị của hai hàm số đối xứng với nhau qua trục Ox.
Bài 5 trang 37 sgk Toán 9 tập 2
Bài 5. Cho ba hàm số:
(y = {1 over 2}{x^2};y = {x^2};y = 2{x^2})
a) Vẽ đồ thị của ba hàm số này trên cùng một mặt phẳng tọa độ.
b) Tìm ba điểm (A, B, C) có cùng hoành độ (x = -1,5) theo thứ tự nằm trên ba đồ thị. Xác định tung độ tương ứng của chúng.
c) Tìm ba điểm (A’, B’, C’) có cùng hoành độ (x = 1,5) theo thứ tự nằm trên ba đồ thị. Kiểm tra tính đối xứng của A và A’, B và B’, C và C’.
d) Với mỗi hàm số trên, hãy tìm giá trị của x để hàm số đó có giá trị nhỏ nhất.
Bài giải:
a) Vẽ đồ thị

b) Gọi ({y_A},{y_B},{y_C}) lần lượt là tung độ các điểm (A, B, C) có cùng hoành độ (x = -1,5). Ta có:
(eqalign{
& {y_A} = {1 over 2}{( – 1,5)^2} = {1 over 2}.2,25 = 1,125 cr
& {y_B} = {( – 1,5)^2} = 2,25 cr
& {y_C} = 2{( – 1.5)^2} = 2.2,25 = 4,5 cr} )
c) Gọi ({y_{A’}},{y_{B’}},{y_{C’}}) lần lượt là tung độ các điểm (A’, B’, C’) có cùng hoành độ (x = 1,5). Ta có:
(eqalign{
& {y_{A’}} = {1 over 2}{(1,5)^2} = {1 over 2}.2,25 = 1,125 cr
& {y_{B’}} = {(1,5)^2} = 2,25 cr
& {y_{C’}} = 2{(1.5)^2} = 2.2,25 = 4,5 cr} )
Kiểm tra tính đối xứng: A và A’, B và B’, C và C’ đối xứng với nhau qua trục tung Oy.
d) Với mỗi hàm số đã cho ta đều có hệ số (a > 0) nên O là điểm thấp nhất của đồ thị.
Vậy (x = 0) thì hàm số có giả trị nhỏ nhất.
Bài 6 trang 38 sgk Toán 9 tập 2
Bài 6. Cho hàm số (y = f(x) = {x^2}).
a) Vẽ đồ thị của hàm số đó.
b) Tính các giá trị (f(-8); f(-1,3); f(-0,75); f(1,5)).
c) Dùng đồ thị để ước lượng các giá trị ({(0,5)^2};{( – 1,5)^2};{(2,5)^2}).
d) Dùng đồ thị để ước lượng vị trí các điểm trên trục hoành biểu diễn các số (sqrt{3}; sqrt{7}).
Bài giải:
a) Vẽ đồ thị hàm số y = x2.

b) Ta có (y = f(x) = {x^2}) nên
(eqalign{
& fleft( { – 8} right){rm{ }} = {rm{ }}{left( { – 8} right)^2} = {rm{ }}64;{rm{ }}fleft( { – 1,3} right){rm{ }} = {rm{ }}{left( { – 1,3} right)^2} = {rm{ }}1,69;{rm{ }} cr
& fleft( { – 0,75} right){rm{ }} = {rm{ }}{left( { – 0,75} right)^2} = {rm{ }}0,5625; cr
& {rm{ }}fleft( {1,5} right){rm{ }} = {rm{ }}1,{5^2} = {rm{ }}2,25 cr} )
c) Theo đồ thị ta có:
(eqalign{
& {(0,5)^2} approx 0,25 cr
& {( – 1,5)^2} approx 2,25 cr
& {(2,5)^2} approx 6,25 cr} )
d) Theo đồ thị ta có: Điểm trên trục hoành (sqrt{3}) thì có tung độ là (y = {(sqrt 3 )^2} = 3). Suy ra điểm biểu diễn (sqrt{3}) trên trục hoành bằng( 1,7). Tương tự điểm biểu diễn (sqrt{7}) gồm bằng (2,7).
Trường
Đăng bởi: Thcs-thptlongphu.edu.vn
Chuyên mục: Tổng hợp





