Giải bài 53, 54, 55 trang 13, 14 SBT Toán 9 tập 1

Giải bài tập trang 13, 14 bài 5 bảng căn bậc hai Sách bài tập (SBT) Toán 9 tập 1. Câu 53: Chứng minh…

Câu 53 trang 13 Sách Bài Tập (SBT) Toán 9 Tập 1

Chứng minh:

a) Số (sqrt 3 ) là số vô tỉ;

Bạn đang xem: Giải bài 53, 54, 55 trang 13, 14 SBT Toán 9 tập 1

b) Các số (5sqrt 2 ); (5sqrt 2 ) đều là số vô tỉ.

Gợi ý làm bài

a) Giả sử (sqrt 3 ) không phải là số vô tỉ. Khi đó tồn tại các số nguyên a và b sao cho (sqrt 3  = {a over b}) với b > 0. Hai số a và b không có ước chung nào khác 1 và -1.

Ta có: ({left( {sqrt 3 } right)^2} = {left( {{a over b}} right)^2}) hay ({a^2} = 3{b^2}) (1)

Kết quả trên chứng tỏ a chia hết cho 3, nghĩa là ta có a = 3c với c là số nguyên.

Thay a = 3c vào (1) ta được: ({left( {3c} right)^2} = 3{b^2}) hay ({b^2} = 3{c^2})

Kết quả trên chứng tỏ a chia hết cho 3, trái với giả thiết a và b không có ước chung nào khác 1 và -1.

Vậy (sqrt 3 ) là số vô tỉ.

b) *Giả sử (5sqrt 2 ) là số hữu tỉ a, nghĩa là số số hữu tỉ x mà (5sqrt 2  = a.)

Suy ra: (sqrt 2  = {a over 5}) hay (sqrt 2 ) là số hữu tỉ.

Điều này vô lí vì (sqrt 2 ) là số vô tỉ.

Vậy (5sqrt 2 ) là số vô tỉ.

*Giả sử (3 + sqrt 2 ) là số hữu tỉ b, nghĩa là số số hữu tỉ b mà:

(3 + sqrt 2  = b)

Suy ra: (sqrt 2  = b – 3) hay (sqrt 2 ) là số hữu tỉ.

Điều này vô lí vì (sqrt 2 ) là số vô tỉ.

Vậy (3 + sqrt 2 ) là số vô tỉ.

Câu 54 trang 14 Sách Bài Tập (SBT) Toán 9 Tập 1

Tìm tập hợp các số x thỏa mãn bất đẳng thức:

(sqrt x  > 2)

Và biểu diễn tập hợp đó trên trục số.

Gợi ý làm bài

Điều kiện: x > 0

Ta có: (sqrt x   sqrt 4  Leftrightarrow x > 4) 

Câu 55 trang 14 Sách Bài Tập (SBT) Toán 9 Tập 1

Tìm tập hợp các số x thỏa mãn bất đẳng thức:

(sqrt x  

Và biểu diễn tập hợp đó trên trục số.

Gợi ý làm bài

Điều kiện: (x ge 0)

Ta có: (sqrt x  

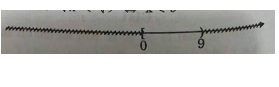
Trường

Giải bài tập