Giải bài 71, 72, 73, 74 trang 147 SBT Toán lớp 7 tập 1

Giải bài tập trang 147 bài 6 tam giác cân Sách Bài Tập Toán lớp 7 tập 1. Câu 71: Vẽ lại hình bên vào vở rồi đặt bài toán vẽ tam giác để có hình bên…

Câu 71 trang 147 Sách Bài Tập (SBT) Toán lớp 7 tập 1

Vẽ lại hình bên vào vở rồi đặt bài toán vẽ tam giác để có hình bên.

Giải

Bạn đang xem: Giải bài 71, 72, 73, 74 trang 147 SBT Toán lớp 7 tập 1

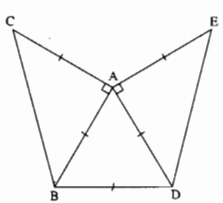
– Vẽ tam giác ABC vuông cân tại A

– Vẽ tam giác đều ABD sao cho D và C nằm trên hai nửa mặt phẳng đối nhau có bờ chứa đường thẳng AB

– Vẽ tam giác vuông cân ADE sao cho E và B nằm trên 2 nửa mặt phẳng đối bờ chứa đường thẳng AD.

Câu 72 trang 147 Sách Bài Tập (SBT) Toán lớp 7 tập 1

Cho tam giác ABC cân tại A. Trên tia đối của tia BC lấy điểm D, trên tia đối của tia CB lấy điểm E sao cho BD = CE. Chứng minh rằng ∆ADE là tam giác cân.

Giải

Ta có: ∆ABC cân tại A

Suy ra: (widehat {{B_1}} = widehat {{C_1}}) (tính chất tam giác cân)

Lại có: (widehat {{B_1}} + widehat {{B_2}} = 180^circ ) (kề bù)

             (widehat {{C_1}} + widehat {{C_2}} = 180^circ ) (kề bù)

Suy ra: (widehat {{B_2}} = widehat {{C_2}})

Xét ∆ABD và ∆ACE, ta có:

AB = AC (gt)

(widehat {{B_2}} = widehat {{C_2}}) (chứng minh trên)

BD = CE (gt)

Suy ra: ∆ABD = ∆ACE (c.g.c)

( Rightarrow ) AD = AE (2 cạnh tương ứng)

Vậy ∆ADE cân tại A (theo định nghĩa tam giác cân)

Câu 73 trang 147 Sách Bài Tập (SBT) Toán lớp 7 tập 1

Cho tam giác ABC. Tia phân giác của góc B cắt ở AC ở D. Trên tia đối của tia BA lấy E sao cho BE = BC. Chứng minh rằng BD // EC.

Giải

Ta có: BD là tia phân giác của (widehat {ABC}left( {gt} right))

Suy ra: (widehat {{B_1}} = widehat {{B_2}} = {1 over 2}widehat {ABC})

Lại có: BE =  BC (gt)

( Rightarrow ) ∆BEC cân tại B (theo định nghĩa)

( Rightarrow ) (widehat E = widehat {BCE}) (tính chất tam giác cân)

∆BEC ta có (widehat {ABC}) là góc ngoài tại đỉnh B

( Rightarrow widehat {ABC} = widehat E + widehat {BCE}) (tính chất góc ngoài của tam giác)

Suy ra: (widehat {ABC} = 2widehat E)

Hay (widehat E = widehat {{B_1}} = {1 over 2}widehat {ABC})

Vậy BD // CE (vì có cặp góc ở vị trí đồng vị như nhau)

Câu 74 trang 147 Sách Bài Tập (SBT) Toán lớp 7 tập 1

Tính số đo các góc của tam giác ACD như hình bên.

Giải

Ta có: ∆ABC vuông cân tại A

Suy ra: (widehat {ABC} = widehat {ACB} = 45^circ )

Lại có: ∆BCD cân tại B (BC = BD)

Suy ra: (widehat {BC{rm{D}}} = widehat D) (tính chất tam giác cân)

Trong ∆BCD ta có (widehat {ABC}) góc ngoài tại đỉnh B

Do vậy: (widehat {ABC} = widehat {BC{rm{D}}} + widehat D) (tính chất góc ngoài của tam giác)

Suy ra: (widehat {ABC} = 2widehat {BC{rm{D}}})

            ( Rightarrow widehat {BC{rm{D}}} = {{45^circ } over 2} = 22^circ 30’)

Vậy: (widehat {AC{rm{D}}} = widehat {ACB} + widehat {BC{rm{D}}} = 45^circ  + 22^circ 30′ = 67^circ 30’)

Trường

Giải bài tập