Giải bài 9, 10, 11, 12 trang 104 SBT Toán 9 tập 1

Giải bài tập trang 104 bài 1 một số hệ thức về cạnh và đường cao trong tam giác vuông Sách bài tập (SBT) Toán 9 tập 1. Câu 9: Một tam giác vuông có cạnh huyền là 5 và đường cao ứng với cạnh huyền là 2. Hãy tính cạnh nhỏ nhất của tam giác vuông này…

Câu 9 trang 104 Sách Bài Tập (SBT) Toán 9 Tập 1

Một tam giác vuông có cạnh huyền là 5 và đường cao ứng với cạnh huyền là 2. Hãy tính cạnh nhỏ nhất của tam giác vuông này.

Gợi ý làm bài:

Bạn đang xem: Giải bài 9, 10, 11, 12 trang 104 SBT Toán 9 tập 1

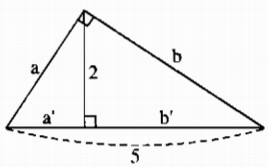
Giả sử tam giác ABC có (widehat {BAC} = {90^0},AH bot BC,BC = 5,AH = 2) và (BH

Ta có: (BH + CH = 5)  (1)

Theo hệ thức liên hệ giữa đường cao và cạnh huyền trong tam giác, ta có:

(BH.CH = A{H^2} = {2^2} = 4)    (2)

Từ (1) và (2) suy ra: (BH = 1) và (CH = 4)

Theo hệ thức liên hệ giữa cạnh góc vuông và hình chiếu, ta có:

(A{B^2} = BH.BC = 1.5 = 5)

Suy ra: (AB = sqrt 5 ).

Câu 10. Trang 104 Sách Bài Tập (SBT) Toán 9 Tập 1

Cho một tam giác vuông. Biết tỷ số hai cạnh góc vuông là 3 : 4 và cạnh huyền là 125cm. Tính độ dài các cạnh góc vuông và hình chiếu của các cạnh góc vuông trên cạnh huyền. 

Gợi ý làm bài:

Giả sử tam giác ABC có (widehat {BAC} = {90^0 },AH bot BC,BC = 125cm,{{AB} over {AC}} = {3 over 4})

Từ ({{AB} over {AC}} = {3 over 4}) suy ra: ({{AB} over 3} = {{AC} over 4} Rightarrow {{A{B^2}} over 9} = {{A{C^2}} over {16}})

Theo tính chất dãy tỉ số bằng nhau,ta có:  

({{A{B^2}} over 9} = {{A{C^2}} over {16}} = {{A{B^2} + A{C^2}} over {9 + 16}} = {{A{B^2} + A{C^2}} over {25}})          (1)

Theo định lí Pi-ta-go, ta có:

(eqalign{
& B{C^2} = A{B^2} + A{C^2} cr 
& Rightarrow A{B^2} + A{C^2} = {125^2} = 15625 cr} )            (2)

Từ (1) và (2) suy ra: ({{A{B^2}} over 9} = {{A{C^2}} over {16}} = {{15625} over {25}} = 625)              (3)

Từ (3) suy ra :

(A{B^2} = 9.625 = 5625 Rightarrow AB = sqrt {5625}  = 75(cm))

(A{C^2} = 16.625 = 10000 Rightarrow AB = sqrt {10000}  = 100(cm)) 

Theo hệ thức liên hệ giữa cạnh góc vuông và hình chiếu, ta có:

(A{B^2} = BH.BC Rightarrow BH = {{A{B^2}} over {BC}} = {{{{75}^2}} over {125}} = 45(cm))

(CH = BC – BH = 125 – 45 = 80(cm))

Câu 11. Trang 104 Sách Bài Tập (SBT) Toán 9 Tập 1

Cho tam giác ABC vuông tại A. Biết rằng ({{AB} over {AC}} = {5 over 6}), đường cao (AH = 30cm). Tính HB, HC.

Gợi ý làm bài:

Xét hai tam giác vuông AHB và CHA, ta có:

(widehat {AHB} = widehat {CHA} = {90^0})

(widehat {ABH} = widehat {CAH}) (hai góc cùng phụ (widehat {ACB}))

Vậy ∆AHB đồng dạng ∆CHA (g.g)

Suy ra: ({{AH} over {HC}} = {{AB} over {CA}}.)                (1)

Theo đề bài: ({{AB} over {AC}} = {5 over 6}) và (AH = 30(cm))           (2)

Từ (1) và (2) suy ra: ({{30} over {HC}} = {5 over 6} Rightarrow HC = {{30.6} over 5} = 36(cm))

Theo hệ thức liên hệ giữa đường cao và hình chiếu, ta có:

(A{H^2} = HB.HC Rightarrow HB = {{A{H^2}} over {HC}} = {{{{30}^2}} over {36}} = 25(cm))

Câu 12. Trang 104 Sách Bài Tập (SBT) Toán 9 Tập 1

Hai vệ tinh đang bay ở vị trí A và B cùng cách mặt đất 230km có nhìn thấy nhau hay không nếu khoảng cách giữa chúng theo đường thẳng là 2200km? Biết rằng bán kính R của Trái Đất gần bằng 6370km và hai vệ tinh nhìn thấy nhau nếu OH > R.

Gợi ý làm bài:

Vì hai vệ tinh cùng cách mặt đất 230km nên tam giác AOB cân tại O.

  Ta có: (OA = R + 230)

( = 6370 + 230 = 6600(km)) 

Trong tam giác AOB ta có: (OA bot AB)

Suy ra: (HA = HB = {{AB} over 2} = {{2200} over 2} = 1100(km))

Áp dụng định lí Pi-ta-go vào tam giác vuông AHO ta có: (A{O^2} = A{H^2} + O{H^2})

Suy ra: (O{H^2} = O{A^2} – A{H^2})

Suy ra:

(eqalign{
& OH = sqrt {O{A^2} – A{H^2}} cr 
& = sqrt {{{6600}^2} – {{1100}^2}} = sqrt {42350000} approx 6508(km) cr} ) 

Vì (OH > R) nên hai vệ tinh nhìn thấy nhau.

Trường

Giải bài tập