Giải bài 92, 93, 94, 95 trang 121, 122 SBT Toán 9 tập 1

Giải bài tập trang 121, 122 bài ôn tập chương I – hệ thức lượng trong tam giác vuông Sách bài tập (SBT) Toán 9 tập 1. Câu 92: Cho tam giác ABC. Biết : AB = 21cm, AC = 28cm, BC = 35cm…

Câu 92 trang 121 Sách Bài Tập (SBT) Toán 9 Tập 1

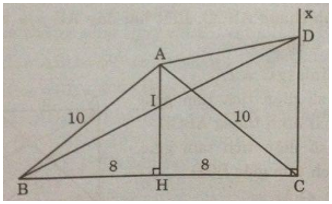
Cho tam giác cân ABC, AB = AC = 10cm, BC = 16cm. Trên đường cao AH lấy điểm I sao cho $AI = {1 over 3}AH$. Vẽ tia Cx song song với AH, Cx cắt tia BI tại D.

a) Tính các góc của tam giác ABC.

Bạn đang xem: Giải bài 92, 93, 94, 95 trang 121, 122 SBT Toán 9 tập 1

b) Tính diện tích tứ giác ABCD.

Gợi ý làm bài

Ta có: (AH bot BC), suy ra: (HB = HC = {{BC} over 2} = 8,(cm))

Trong tam giác vuông ABH, ta có: 

(cos widehat B = {{HB} over {AB}} = {8 over {10}} = 0,8)

Suy ra: (widehat B approx 36^circ 52’)

Vì ∆ABC cân nên (widehat B = widehat C = 36^circ 52’)

Ta có: 

(widehat A = 180^circ  – (widehat B + widehat C) = 180^circ  – (36^circ 52′ + 36^circ 52′) = 106^circ 16’)

b) Áp dụng định lí Pi-ta-go vào tam giác vuông ABH, ta có:

(eqalign{
& A{B^2} = A{H^2} + B{H^2} cr 
& Rightarrow A{H^2} = A{B^2} – B{H^2} = {10^2} – {8^2} = 36 cr} )

Suy ra: AH = 6 (cm)

Ta có: (AI = {1 over 3}.AH = {1 over 3}.6 = 2,(cm))

Suy ra: IH = AH – AI = 6 – 2 = 4 (cm)

Vì (IH bot BC) và $DC bot BC$ nên IH // DC (1)

Mặt khác: BH = HC (gt)  (2)

Từ (1) và (2) ta có IH là đường trung bình của tam giác BCD

Suy ra: (IH = {1 over 2}CD) hay CD = 2IH = 2.4 = 8 (cm)

Ta có:  

({S_{ABH}} = {1 over 2}AH.BH = {1 over 2}.6.8 = 24,,left( {c{m^2}} right))

({S_{AHCD}} = {{AH + CD} over 2}.HC = {{6 + 8} over 2}.8 = 56,left( {c{m^2}} right))

Vậy ({S_{ABCD}} = S{  _{ABH}} + {S_{AHCD}} = 24 + 56 = 80,) (cm²)

 

---

Câu 93 trang 121 Sách Bài Tập (SBT) Toán 9 Tập 1

Cho tam giác ABC. Biết : AB = 21cm, AC = 28cm, BC = 35cm.

a) Chứng minh tam giác ABC vuông.

b) Tính sinB, sinC.

Gợi ý làm bài

a) Ta có: (A{B^2} = {21^2} = 441)

(A{C^2} = {28^2} = 784)

(B{C^2} = {35^2} = 1225)

Vì (A{B^2} + A{C^2} = 441 + 784 = 1225 = B{C^2})  nên tam giác ABC vuông tại A ( theo định lí đảo Pi-ta-go).

b) Ta có: 

(sin widehat B = {{AC} over {BC}} = {{28} over {35}} = {4 over 5} = 0,8)

(sin widehat C = {{AB} over {BC}} = {{21} over {35}} = {3 over 5} = 0,6)

 

---

Câu 94 trang 122 Sách Bài Tập (SBT) Toán 9 Tập 1

Cho hình thang ABCD. Biết hai đáy AB = a và CD = 2a, cạnh bên AD = a, (widehat A = 90^circ )

a) Chứng minh (tgwidehat C = 1.)

b) Tính tỉ số diện tích tam giác BCD và diện tích hình thang ABCD.

c) Tính tỉ số diện tích tam giác ABC và diện tích tam giác BCD.

Gợi ý làm bài

a) Kẻ (BH bot CD)

Ta có: AB // CD và (widehat A = 90^circ )

Suy ra: (widehat D = 90^circ )

Tứ giác ABHD có ba góc vuông và AB = AD = a nên là hình vuông.

Suy ra: DH = BH = AB = a

Ta có: CD = DH + HC

Suy ra: HC = CD – DH = 2a – a = a

Vậy (tgwidehat C = {{BH} over {CH}} = {a over a} = 1)

b) Ta có: ({S_{BCD}} = {1 over 2}BH.CD = {1 over 2}a.2a = {a^2}) (đvdt)

({S_{ABCD}} = {{AB + CD} over 2}.AD = {{a + 2a} over 2}.a = {3 over 2}{a^2}) (đvdt)

Vậy ({{{S_{BCD}}} over {{S_{ABCD}}}} = {{{a^2}} over {{3 over 2}{a^2}}} = {1 over {{3 over 2}}} = {2 over 3}.)

c) Ta có: ({S_{ABC}} = {1 over 2}a.a = {1 over 2}{a^2}) (đvdt)

Vậy ({{{S_{ABC}}} over {{S_{BCD}}}} = {{{1 over 2}{a^2}} over {{a^2}}} = {1 over 2})

 

---

Câu 95 trang 122 Sách Bài Tập (SBT) Toán 9 Tập 1

Cho tam giác ABC có góc B bằng (120^circ ), BC = 12cm, AB = 6cm. đường phân giác của góc B cắt cạnh AC tại D.

a) Tính độ dài đường phân giác BD.

b) Gọi M là trung điểm của BC. Chứng minh (AM bot BD.)

Gợi ý làm bài

a) Ta có: 

(widehat {ABD} = widehat {CBD} = {{widehat {ABC}} over 2} = {{120^circ } over 2} = 60^circ )

Từ A kẻ đường thẳng song song với BD cắt CD tại E.

Lại có:

(widehat {BAE} = widehat {ABD} = 60^circ ) (so le trong)

 

(widehat {CBD} = widehat {AEB} = 60^circ ) (đồng vị)

Suy ra tam giác ABE  đều 

( Rightarrow AB = BE = EA = 6,(cm),,(1))

Khi đó: CE = BC + BE = 12 + 6 = 18 (cm)

Tam giác ACE có AE // BD nên suy ra:

(eqalign{
& {{BC} over {CE}} = {{BD} over {AE}} cr 
& Rightarrow BD = {{BC.AE} over {CE}} = {{12.6} over {18}} = 4,(cm) cr} )

b) Ta có: 

(MB = MC = {1 over 2}.BC = {1 over 2}.12 = 6,(cm),,(2))

Từ (1) và (2) suy ra:

(BM = AB Rightarrow ) ∆ABM cân tại B.

Tam giác cân ABM có BD là đường phân giác nên đồng thời nó cũng là đường cao (tính chất tam giác cân). Vậy (BD bot AM)

Trường

Giải bài tập