Giải bài 15, 16, 17, 18, 19 trang 114 SGK Toán 7

Giải bài tập trang 114 bài 3 Trường hợp bằng nhau thứ nhất của tam giác: cạnh – cạnh – cạnh (c.c.c) Sách giáo khoa (SGK) Toán 7. Câu 15: Vẽ tam giác…

Bài 15 trang 114 – Sách giáo khoa toán 7 tập 1

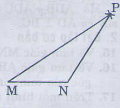
Vẽ tam giác (MNP), biết (MN=2,5 cm, NP=3cm, PM= 5cm)

Giải:

Bạn đang xem: Giải bài 15, 16, 17, 18, 19 trang 114 SGK Toán 7

-Vẽ đoạn (MN= 2,5cm)

– Trên cùng một nửa mặt phẳng bờ (MN) vẽ cung tròn tâm (M) bán kính (5cm) và cung tròn tâm (N) bán kinh (3cm).

– Hai cung tròn cắt nhau tại (P). Vẽ các đoạn (MN, NP), ta được tam giác (MNP).

Bài 16 trang 114 – Sách giáo khoa toán 7 tập 1

Vẽ tam giác biết độ dài mỗi cạnh là (3) cm. Sau đó đo góc của mỗi tam  giác.

Giải.

– Vẽ đoạn thẳng (AB=3,cm)

– Trên cùng một nửa mặt phẳng bờ (AB) vẽ cung tròn tâm (A) bán kính (3,cm) và cung tròn tâm (B) bán kính (3,cm)

– Hai cung tròn cắt nhau tại (C)

– Vẽ các đoạn thẳng (AC, BC); ta được tam giác (ABC) 

– Đo mỗi góc của tam giác (ABC) ta được:

(widehat{A}=widehat{B}=widehat{C}= 60^0)

Bài 17 trang 114 – Sách giáo khoa toán 7 tập 1

Trên mỗi hình sau có tam giác nào bằng nhau? Vì sao?

Giải

*  Hình a.

Ta có: AB=AB(cạnh chung)

          AC= AD(gt)

          BC=BD(gt)

vậy ∆ABC= ∆ABD(c.c.c)
* Hình b.

Ta có: 

∆MNQ=∆QPM(c.c.c)

vì MN=QP(gt)

NQ=PM(gt)

MQ=QM(cạnh chung)

* Hình c.

Ta có:

∆EHI=∆IKE(c.c.c) vì

EH=IK(gt)

HI=KE(gt)

EI=IE(gt)

+ ∆EHK=∆IKH(c.c.c) vì

EH=IK(gt)

EK=IH(gt)

HK=KH(cạnh chung)

Bài 18 trang 114 – Sách giáo khoa toán 7 tập 1

Xét bài toán: “(Delta AMB) và (Delta ANB) có (MA=MB, NA=NB) (h.71). Chứng minh rằng

(widehat{AMN}=widehat{BMN}).”

1) Hãy ghi giả thiết và kết luận của bài toán.

2) Hãy sắp xếp bốn câu sau đây một cách hợp lý để giải bài toán trên :

a) Do đó  (Delta AMN=Delta BMN (c.c.c))

b)

(MN) cạnh chung

(MA=MB) ( Giả thiết)

(NA= NB) ( Giả thiết)

c) Suy ra (widehat{AMN}=widehat{BMN}) (2 góc tương ứng)

d)(Delta AMB) và (Delta ANB) có:

Giải

1)

2) sắp xếp theo thư tự.

d,b,a,c.

Bài 19 trang 114 – Sách giáo khoa toán 7 tập 1

Cho hình 72. Chứng minh rằng:

a) (∆ADE = ∆BDE).

b) (widehat{DAE}=widehat{DBE}).

Giải:

Xem hình vẽ:

a) Xét (∆ADE) và (∆BDE) có:

+) (DE) cạnh chung

+) (AD=BD) (gt)

+) (AE=BE) (gt)

Vậy( ∆ADE=∆BDE) (c.c.c)

b) Từ (∆ADE=∆BDE) (chứng minh trên)

Suy ra (widehat{DAE}=widehat{DBE}) (Hai góc tương ứng)

Trường

Giải bài tập