Giải bài 53, 54, 55, 56 trang 144, 145 SBT Toán lớp 7 tập 1

Giải bài tập trang 144, 145 bài 5 trường hợp bằng nhau thứ nhất của tam giác góc-cạnh-góc (g-c-g) Sách Bài Tập Toán lớp 7 tập 1. Câu 53: Cho tam giác ABC. Các tia phân giác của các góc B và C cắt nhau ở O…

Câu 53 trang 144 Sách Bài Tập (SBT) Toán lớp 7 tập 1

Cho tam giác ABC. Các tia phân giác của các góc B và C cắt nhau ở O. Kẻ ({rm{OD}} bot AC), kẻ ({rm{O}}E bot AB). Chứng minh rằng OD = OE.

Giải

Bạn đang xem: Giải bài 53, 54, 55, 56 trang 144, 145 SBT Toán lớp 7 tập 1

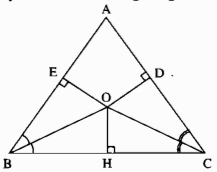
Kẻ (OH bot BC)

Xét hai tam giác vuông OEB và OHB, ta có:

(widehat {OEB} = widehat {OHB} = 90^circ )

Cạnh huyền OB chung

(widehat {EBO} = widehat {HBO}) (gt)

Suy ra: ∆OEB = ∆OHB (cạnh huyền, góc nhọn)

( Rightarrow ) OE = OH (hai cạnh tương ứng)                    (1)

Xét hai tam giác vuông OHC và ODC, ta có:

(widehat {OHC} = widehat {O{rm{D}}C} = 90^circ )

Cạnh huyền OC chung

(widehat {HCO} = widehat {DCO}left( {gt} right))

Suy ra: ∆OHC = ∆ODC (cạnh huyền, góc nhọn)

( Rightarrow ) OH = OD (hai cạnh tương ứng)                     (2)

Từ (1) và (2) suy ra: OE = OD.

Câu 54 trang 144 Sách Bài Tập (SBT) Toán lớp 7 tập 1

Cho tam giác ABC có AB = AC. Lấy điểm D trên cạnh AB, điểm E trên cạnh AC sao cho AD = AE.

a) Chứng minh rằng  BE = CD.

b) Gọi O là giao điểm của BE  và CD. Chứng minh rằng ∆BOD = ∆COE

Giải

a) Xét ∆BEA và ∆CDA, ta có:

BA = CA (gt)

(widehat A) chung

AE = AD (gt)

Suy ra: ∆BEA = ∆CDA (c.g.c)

Vậy BE = CD (hai cạnh tương ứng)

b) ∆BEA = ∆CDA (chứng minh trên)

(Rightarrow widehat {{B_1}} = widehat {{C_1}};widehat {{E_1}} = widehat {{D_1}}) (hai góc tương ứng)

(widehat {{E_1}} + widehat {{E_2}} = 180^circ ) (hai góc kề bù)

(widehat {{D_1}} + widehat {{D_2}} = 180^circ ) (hai góc kề bù)

Suy ra: (widehat {{E_2}} = widehat {{D_2}})

             AB = AC (gt)

( Rightarrow ) AE + EC  =  AD + DB mà AE = AD (gt) => EC = DB

Xét ∆ODB và ∆OCE, ta có:

(widehat {{D_2}} = widehat {{E_2}}) (chứng minh trên)

DB = EC (chứng minh trên)

(widehat {{B_1}} = widehat {{C_1}}) (chứng minh trên)

Suy ra: ∆ODB = ∆OEC (g.c.g)

Câu 55 trang 145 Sách Bài Tập (SBT) Toán lớp 7 tập 1

Cho tam giác ABC có (widehat B = widehat C). Tia phân giác góc A cắt BC tại D. Chứng minh rằng DB = DC, AB = AC.

Giải

Trong ∆ADB, ta có:

(widehat B + widehat {{A_1}} + widehat {{D_1}} = 180^circ ) (tổng ba góc trong tam giác)

Suy ra: (widehat {{D_1}} = 180^circ  – left( {widehat B + widehat {{A_1}}} right))                          (1)

Trong ∆ADC, ta có:

(widehat C + widehat {{D_2}} + widehat {{A_2}} = 180^circ ) (tổng ba góc trong tam giác)

Suy ra: (widehat {{D_2}} = 180^circ  – left( {widehat C + widehat {{A_2}}} right))                          (2)

            (widehat B = widehat Cleft( {gt} right))

            (widehat {{A_1}} = widehat {{A_2}}left( {gt} right))

           (widehat B = widehat Cleft( {gt} right))

Từ (1), (2) và (gt) suy ra: (widehat {{D_1}} = widehat {{D_2}})

Xét ∆ADB và ∆ADC, ta có:

             (widehat {{A_1}} = widehat {{A_2}})

              AD cạnh chung

             (widehat {{D_1}} = widehat {{D_2}}) (chứng minh trên)

Suy ra: ∆ADB = ∆ADC(g.c.g)

Vậy: AB = AC (2 cạnh tương ứng)

         DB = DC (2 cạnh tương ứng)

Câu 56 trang 145 Sách Bài Tập (SBT) Toán lớp 7 tập 1

Cho hình dưới, chứng minh rằng O là trung điểm của mỗi đoạn thẳng AD, BC

Giải

Hai đường thẳng AB và CD tạo với BD có hai góc trong cùng phía bù nhau

(120^circ  + 60^circ  = 180^circ )

Suy ra  AB // CD

Ta có: (widehat A = widehat {{D_1}})           (hai góc trong so le)

            (widehat {{B_1}} = widehat C) (hai góc trong so le)

            AB = CD (gt)

Suy ra: ∆AOB = ∆DOC (g.c.g)

Suy ra: OA = OD; OB = OC (hai cạnh tương ứng)

Vậy O là trung điểm của mỗi đoạn thẳng AD và BC.

Trường

Giải bài tập