Giải bài 71, 72, 73, 74 trang 168, 169 SBT Toán 9 tập 2

Giải bài tập trang 168, 169 bài 8 Vị trí tương đối của hai đường tròn (tiếp theo) Sách bài tập (SBT) Toán 9 tập 2. Câu 71: Hai đường tròn (I) và (B) nói trên có vị trí tương đối như thế nào đối với nhau…

Câu 71 trang 168 Sách bài tập (SBT) Toán 9 Tập 2

Cho I là trung điểm của đoạn thẳng AB. Vẽ các đường tròn (I ; IA) và (B ; BA)

a)      Hai đường tròn (I) và (B) nói trên có vị trí tương đối như thế nào đối với nhau? Vì sao?

Bạn đang xem: Giải bài 71, 72, 73, 74 trang 168, 169 SBT Toán 9 tập 2

b)      Kẻ một đường thẳng đi qua A, cắt các đường tròn (I) và (B) theo thứ tự tại  M và N. So sánh các độ dài AM và MN.

Giải:

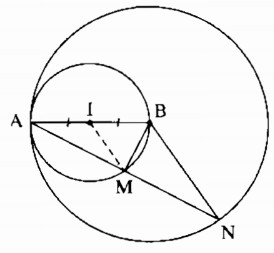
a) Vì A, I , B thẳng hàng nên:

         BI = AB – AI

Vậy đường tròn (I ; IA) tiếp xúc với đường tròn (B; BA) tại A.

b) Tam giác AMB nội tiếp trong đường tròn (I) có AB là đường kính nên (widehat {AMB} = 90^circ )

Suy ra: AM ⊥ BM hay BM ⊥ AN

Suy ra: AM = AN ( đường kính vuông góc dây cung).

Câu 72 trang 169 Sách bài tập (SBT) Toán 9 Tập 2

Cho hai đường tròn đồng tâm O. Gọi AB là dây bất kỳ của đường tròn nhỏ. Đường thẳng AB cắt đường tròn lớn ở C và D ( nằm giữa B và C). So sánh các độ dài AC và BD.

Giải:

Kẻ OI ⊥ AB. Ta có: OI ⊥ CD

Trong đường tròn (O) (nhỏ) ta có: OI ⊥ AB

Suy ra:

IA = IB ( đường kính vuông góc dây cung)                     (1)

Trong đường tròn (O) (lớn) ta có: OI ⊥ CD

Suy ra:

IC = ID ( đường kính vuông góc dây cung)

Hay IA + AC = IB + BD                                                  (2)

Từ (1) và (2) suy ra: AC = BD.

Câu 73 trang 169 Sách bài tập (SBT) Toán 9 Tập 2

Cho hai đường tròn (O) và (O’) tiếp xúc ngoài tại A. Gọi CD là tiếp tuyến chung ngoài của hai đường tròn ( C ∈ (O), D ∈ (O’)).

a)      Tính số đo góc CAD.

b)      Tính độ dài CD biết OA = 4,5cm, O’A = 2cm..

Giải:

a) Kẻ tiếp tuyến  chung tại A cắt CD tại M

Trong đường tròn (O) ta có:

       MA =  MC (tính chất hai tiếp tuyến cắt nhau)

Trong đường tròn (O’) ta có:

       MA =  MD (tính chất hai tiếp tuyến cắt nhau)

Suy ra: (MA = MC = MD = {1 over 2}CD)

Tam giác ACD có đường trung tuyến AM ứng với cạnh CD và bằng nửa cạnh CD nên tam giác ACD vuông tại A

Suy ra: (widehat {CAD} = 90^circ )

b) Ta có:

MO là tia phân giác của (widehat {CMA}) (tính chất hai tiếp tuyến cắt nhau)

MO’ là tia phân giác của (widehat {DMA}) (tính chất hai tiếp tuyến cắt nhau)

Suy ra: MO ⊥ MO’ (tính chất hai góc kề bù)

Tam giác MOO’ vuông tại M có MA ⊥ OO’ ( tính chất tiếp tuyến)

Theo hệ thức lượng trong tam giác vuông, ta có:

MA² = OA.O’A = 4,5.2 = 9 ⇒ MA = 3 (cm)

Mà (MA = {1 over 2}CD ⇒ CD = 2.MA = 2.3 = 6 (cm))

Câu 74 trang 169 Sách bài tập (SBT) Toán 9 Tập 2

Cho hai đường tròn đồng tâm O. Một đường tròn (O’) cắt một đường tròn tâm O tại A, B và cắt đường tròn tâm O còn lại tại C, D. Chứng minh rằng AB // CD.

Giải: 

Vì đường tròn (O’) cắt đường tròn ( O; OA) tại A và B nên OO’ là trung trực của AB

Suy ra: OO’ ⊥ AB         (1)

Vì đường tròn (O’) cắt đường tròn (O; OC) tại C và D nên OO’ là trung trực của CD

Suy ra: OO’ ⊥ CD          (2)

Từ (1) và (2) suy ra: AB // CD.

Trường

Giải bài tập